Equivariance tests

E.3 Equivariance tests

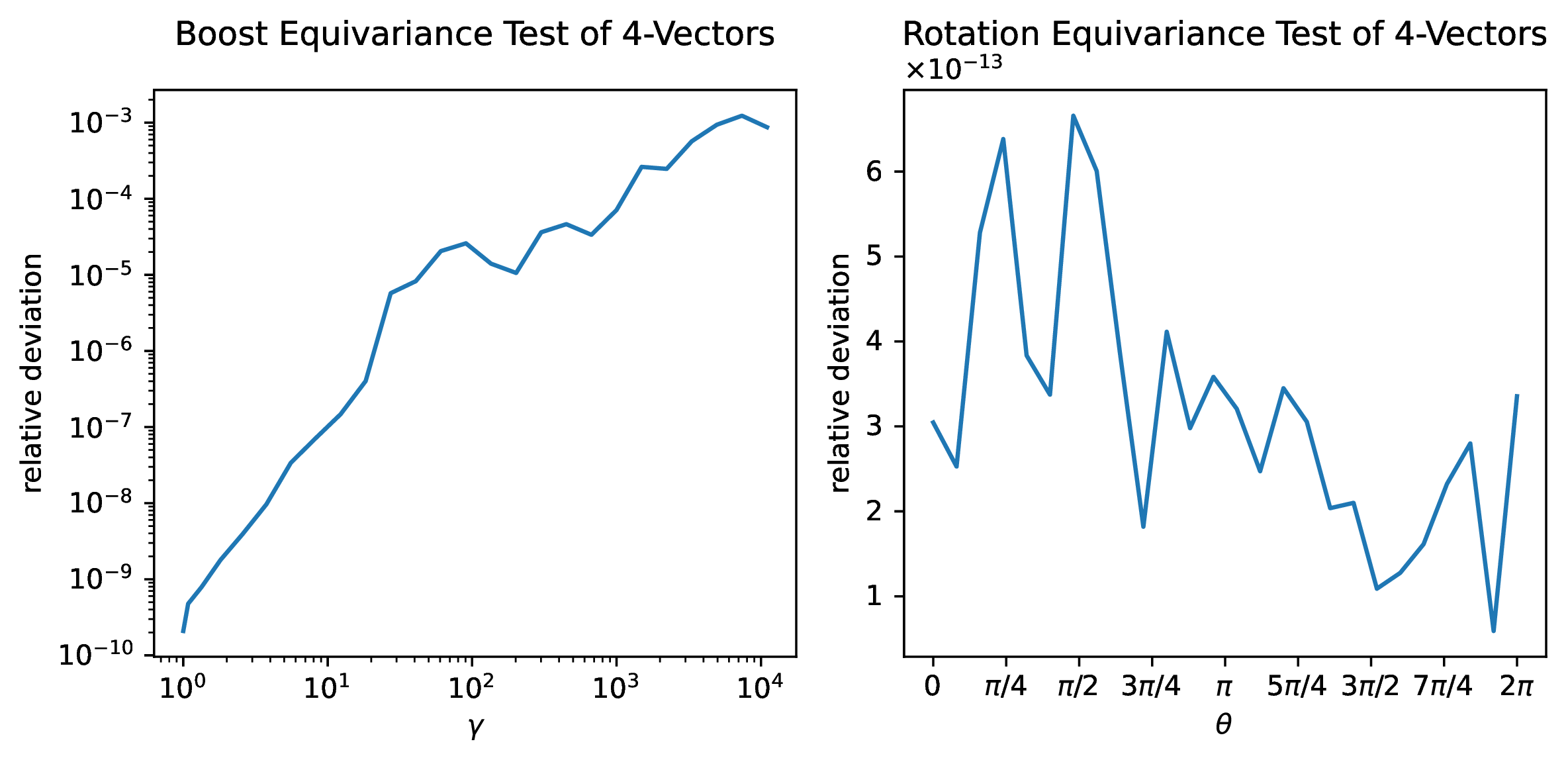
We test the covariance of the LGAE models to Lorentz transformations and find they are indeed equivariant up to numerical errors. Reference [54] points out that equivariance to boosts in particular is sensitive to numerical precision, so we use double precision (64-bit) throughout the model. In addition, we scale down the data by a factor of 1,000 (i.e. working in the units of PeV) for better numerical precision at high boosts.

For a given transformation $Λ \in {SO}^{+} (3, 1)$ we compare $Λ \cdot LGAE (p)$ and $LGAE (Λ \cdot p)$ are compared, where $p$ is the particle-level 4-momentum. The relative deviation is defined as

δ_{p} (Λ) = | \frac{mean (LGAE (Λ \cdot p)) - mean (Λ \cdot LGAE (p))}{mean (Λ \cdot LGAE (p))} |

(E.3.1)

Figure E.2 shows the mean relative deviation, averaged over each particle in each jet, over $3000$ jets from our test dataset from boosts along and rotations around the $z$ -axis. We find the relative deviation from boosts to be within $O (1 0^{- 3})$ in the interval $γ \in [0, \cosh (10)]$ (equivalent to $β \in [0, 1 - 4 \times 1 0^{- 9}$ ]) and from rotations to be $< 1 0^{12}$ .

Figure E.2. The relative deviations, as defined in Eq. E.3.1, of the output 4-momenta $p^{μ}$ to boosts along the $z$ -axis (left) and rotations around the $z$ -axis (right).