D.1 Further Discussion on IPMs vs. $f$-Divergences

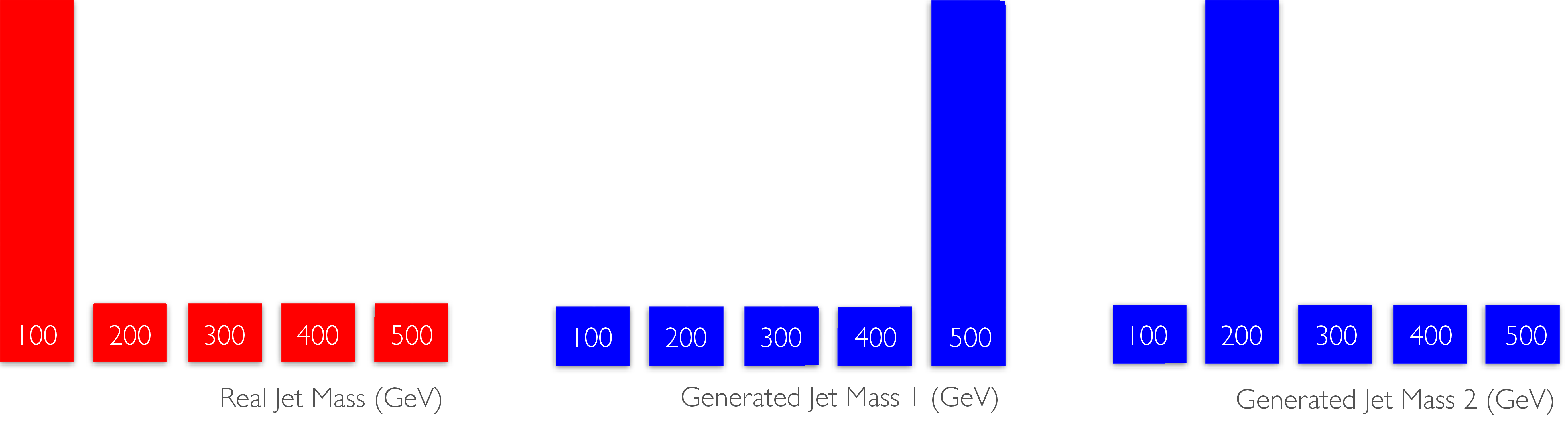
A crucial advantage of IPMs in evaluating generative models is that they consider the metric space of the distributions. We illustrate this with the help of Figure D.1, inspired heavily by Refs. [63, 64], which shows an example real (in red) and two generated (in blue) jet mass distributions. Clearly, in the context of simulation, the second generated distribution contains a peak closer to the real peak and, hence, is a better model. However, because $f$-divergences such as the KL or ${\chi }^2$ look only at the pointwise difference between distributions, they find both generated distributions to be as discrepant with the real. IPMs like the Wasserstein metric or MMD, on the other hand, generally identify the second distribution as being closer to the real.