Further Discussion on Gaussian Dataset Experiments

D.2 Further Discussion on Gaussian Dataset Experiments

Figure D.2. Time taken per each metric on Gaussian-distributed datasets as described in Section 11.2.

Figure D.3. Scores of each metric on Gaussian-distributed datasets as described in Section 11.2.

Figure D.4. Scores of each metric on Gaussian-distributed datasets as described in Section 11.2.

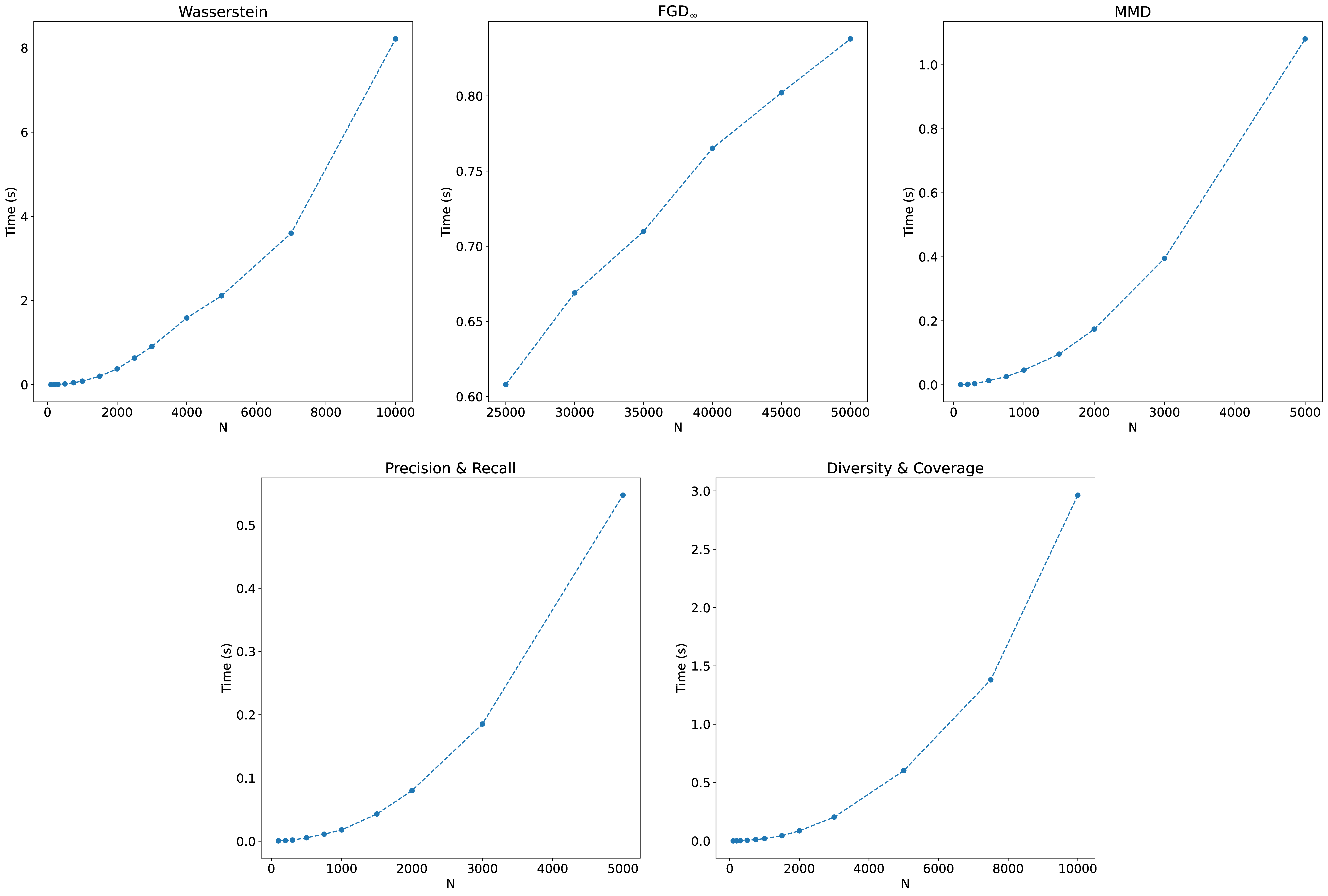
Figure D.2 plots the time taken per measurement of each metric used in Section 11.2 for different sample sizes, measured on an 8-core Intel Core i9 processor. The quadratic scaling of the Wasserstein and diversity and coverage metrics, in combination with their low rate of convergence, means their use for evaluation is practically difficult. MMD and precision and recall exhibit the same scaling; however, are observed to converge within roughly 3000 samples. ${FGD}_{\infty}$ scales linearly and remains fast to compute even at the highest batch size tested.

Figures D.3 and D.4 show measurements of each metric on each distribution discussed in Section 11.2, as well as FGD and MMD with a third-order polynomial kernel for varying samples sizes. We can see from these plots that indeed, as discussed in Refs. [356, 357], FGD is biased, but the solution from Ref. [357] of extrapolating to infinite-sample size ( ${FGD}_{\infty}$ ) largely solves this issue. We also note that, perhaps surprisingly, a third-order polynomial kernel, as used for the KID [356] in computer vision, is not sufficient to discern the mixtures of Gaussian distributions from the single Gaussian. Hence, we recommend a fourth-order kernel for the kernel physics distance.