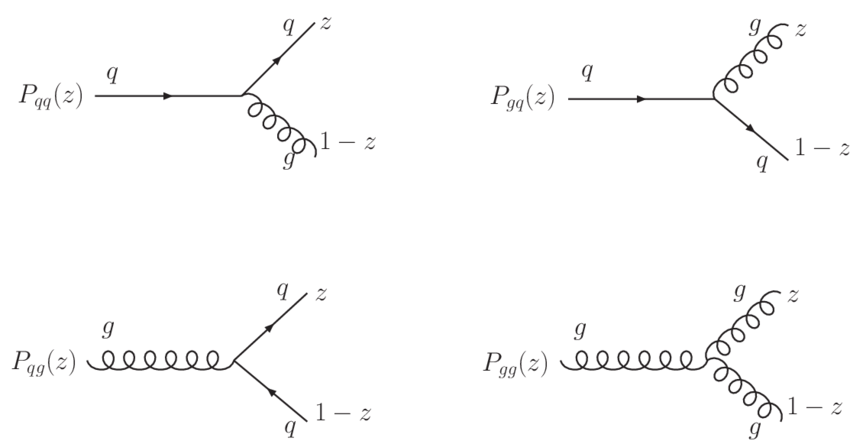4.1 Quantum chromodynamics
Quantum chromodynamics (QCD) is a quantum Yang-Mills field theory describing the strong force, with the gauge group . has eight generators and, hence, eight gauge bosons () called gluons. The only other elementary particles which interact with the strong force — i.e., which don’t live in the trivial representation of — are the quarks. They live in the three-dimensional fundamental representation and thus possess three extra DoFs beyond vanilla spinors, which we call their “color” (hence, quantum chromodynamics). The three orthogonal eigenstates in this representation are colloquially referred to as labeled red, green, and blue, and mathematically the quark fields () labeled with extra color indices .
Putting this together, the QCD Lagrangian, with all the indices labeled explicitly is:
|
| (4.1) |
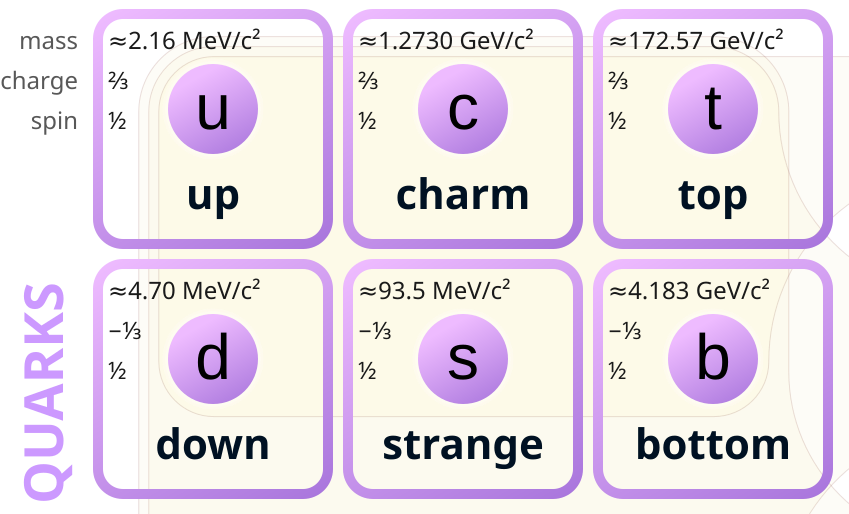
where is the strong coupling constant, is the gluon field strength tensor, are the structure constants of , are the generators of in the fundamental representation, the sum over is running over the six flavors, and the indices and label the eight gluons and the three colors of quarks, respectively. The six flavors of quarks have different masses and charges, as shown in Figure 4.2.
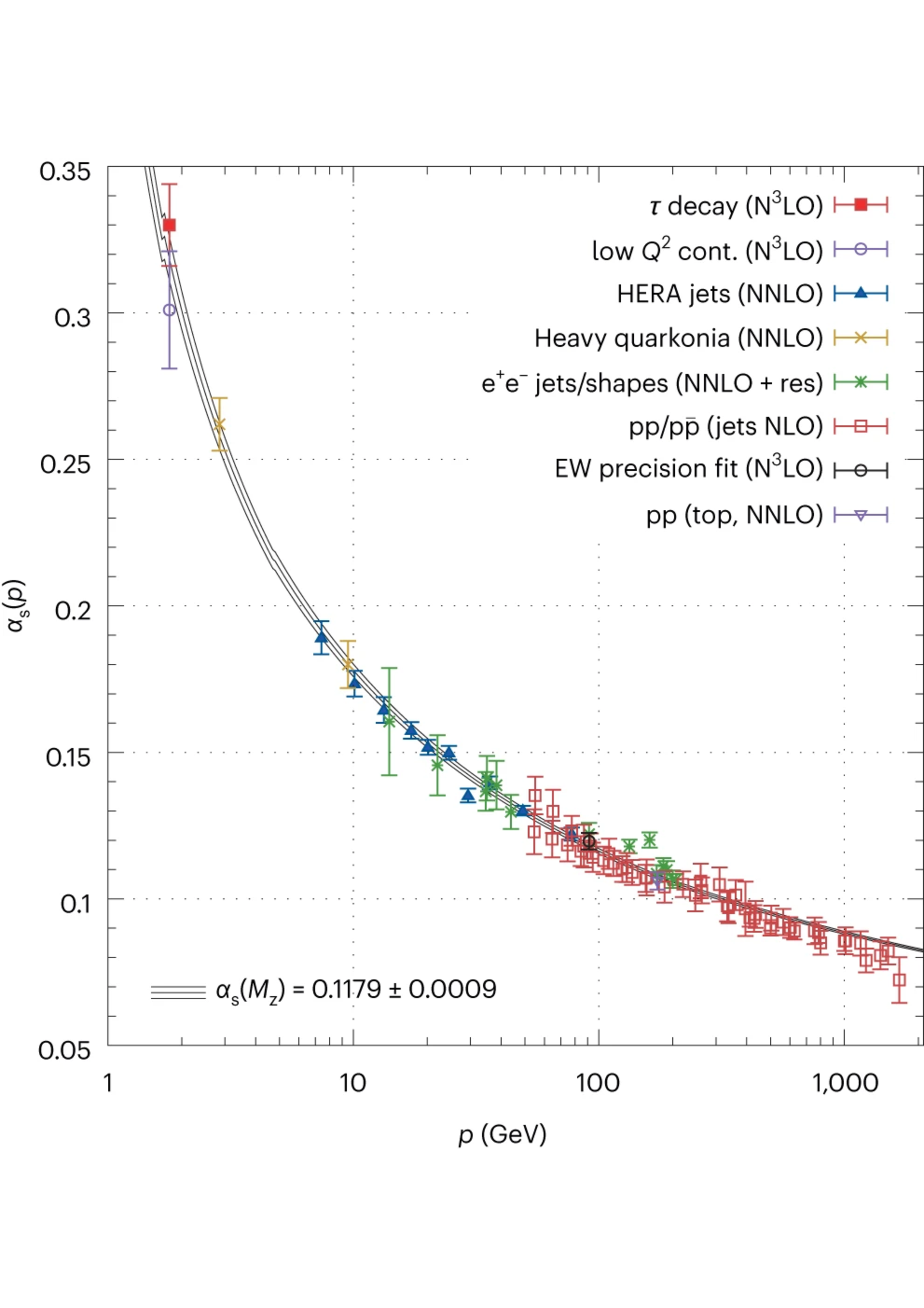
QCD is an extremely rich and complex theory due to its non-abelian gauge symmetry, the six different flavors of quarks, and the unique strength and running of its coupling, shown in Figure 4.3. Observe its property of weak coupling and asymptotic freedom at high energies, versus the extremely high value of at low energies leading to the phenomenon of confinement. Note also that appears to diverge in Figure 4.3 at around , a sign of perturbation theory breaking down. This limit is considered the characteristic energy scale of QCD, .2
The coupling strength means that the standard perturbative techniques we have discussed are not applicable at our usual energy scales; instead, we must rely on nonperturbative techniques such as numerical simulations of QCD on a discretized spacetime lattice (see e.g. Schwartz [16] Chapter 25). Because of this, QCD is one of the least understood and most exciting areas of study in modern physics.
4.1.1 Asymptotic freedom and confinement
As discussed above, a key phenomenological characteristic of the strong force is asymptotic freedom, wherein at high energies quarks and gluons behave as free particles. This also means that perturbative techniques can be applied at high energies; indeed, we can derive an analogous “Coulomb force”, based on tree-level quark-quark scattering amplitudes, for quarks at very short distances. This force turns out to always be attractive between quarks and antiquarks, as well as between two or even three quarks in different color states: the “aim” of the force appears to always be to form color-neutral bound states. These are called mesons for the case of an antiquark and quark pair, and baryons for three quarks.
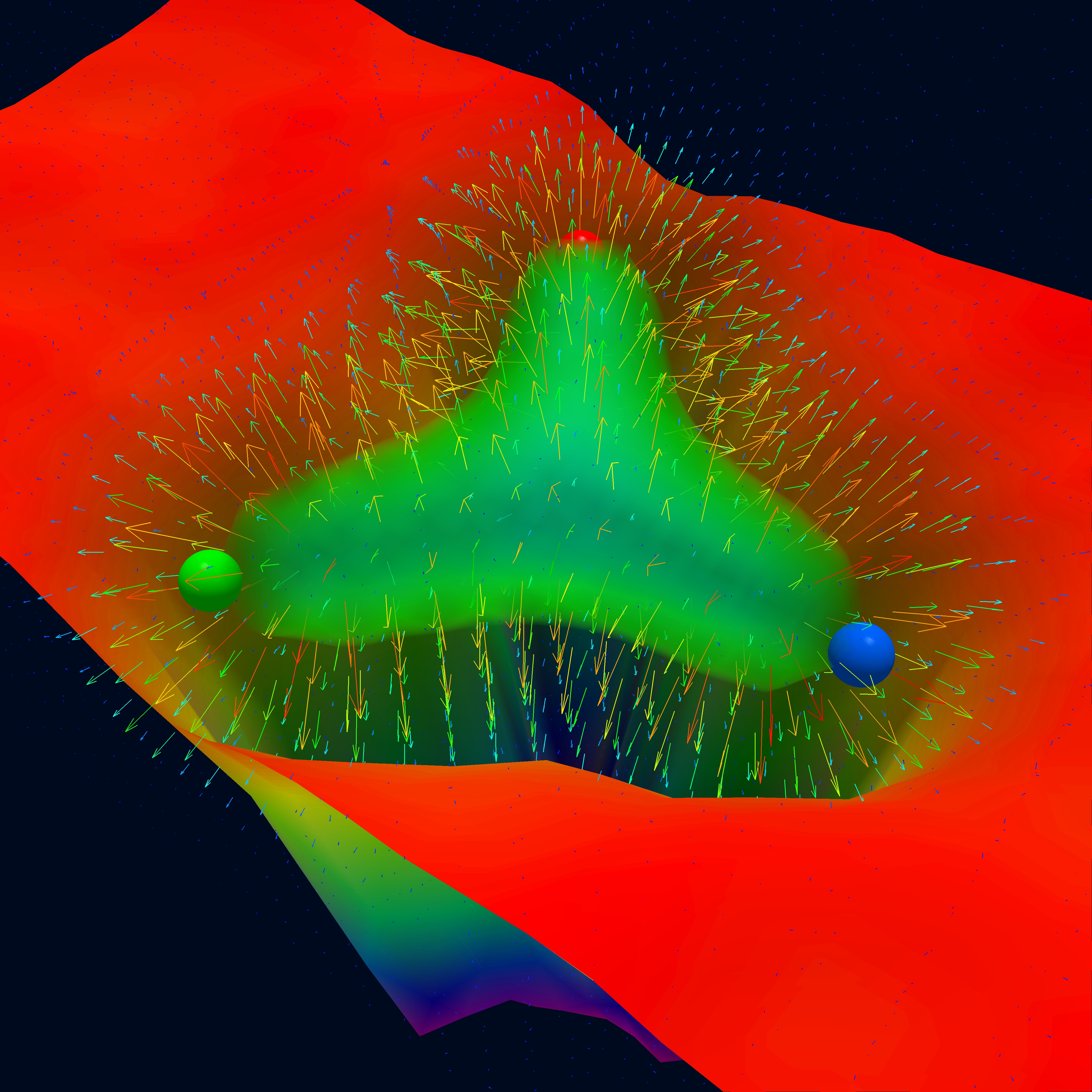
At longer distances we enter the strong-coupling and nonperturbative regime, in which the dynamics are harder to understand. However, through lattice QCD simulations, we are able to see the emergence of a “flux tube” pulling quarks together as they are pushed apart, as shown in Figure 4.4. This phenomenon is referred to as confinement, and it means we can never observe free quarks or gluons outside high-energy colliders. Both the long- and short-distance behavior of the strong force conspire to always confine quarks in color-neutral hadrons. The scale of confinement is naturally set by , which is hence roughly the radius of the proton and other hadrons (fm in SI).
4.1.2 Quarks and the eightfold way
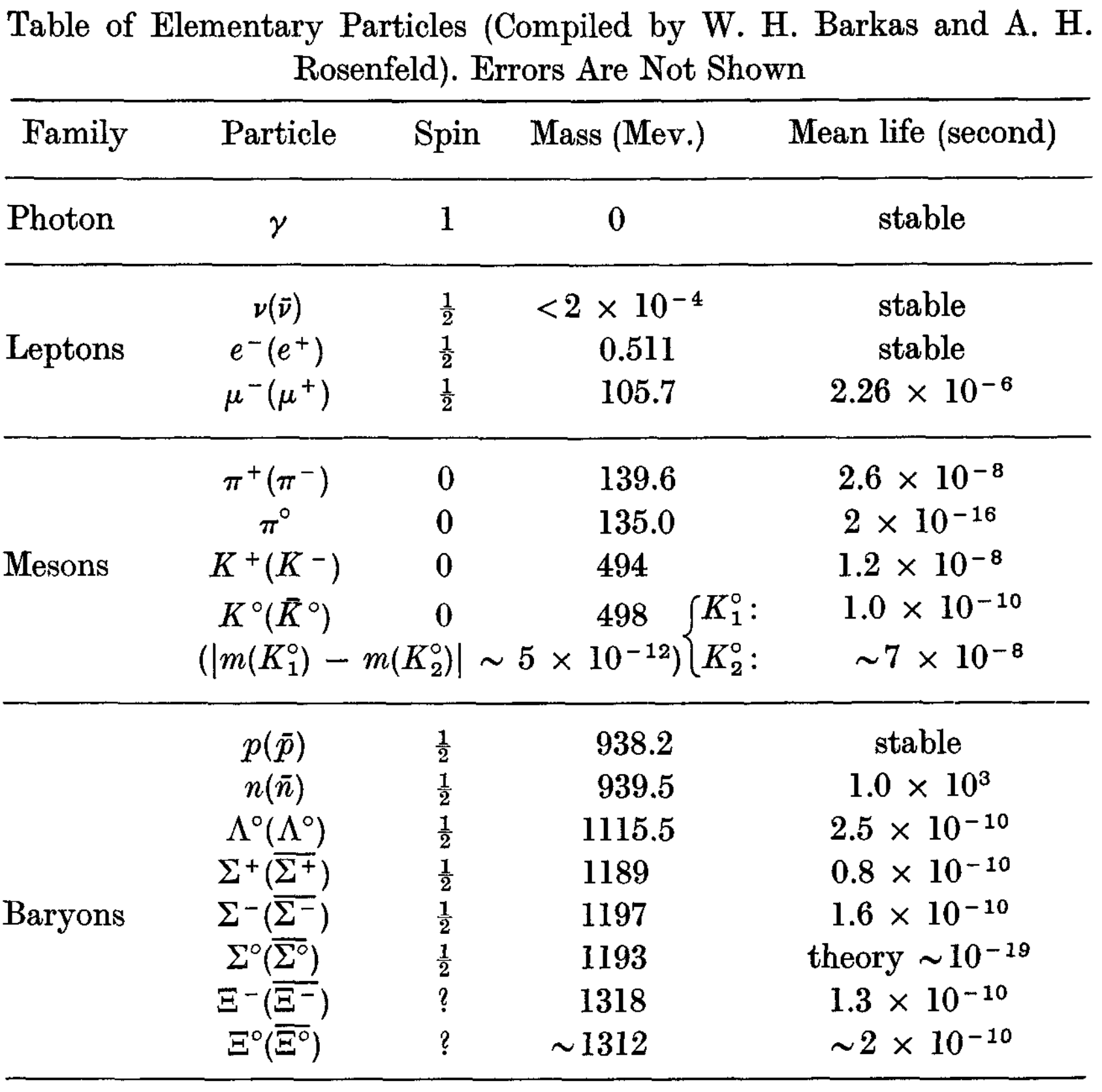
Since their discovery in the 1920s and 30s, the proton and neutron and were believed to be elementary particles along with the electron and photon. In fact, due to confinement, the first experimental evidence of quarks was not found until the 1960s. However, already in 1932, the remarkably similar masses of the two nucleons surprised physicists and led Heisenberg, Wigner, and others to hypothesize an underlying symmetry between them (later named isospin) [75, 76]. The intrigue only increased in the next decades, during which new cosmic ray, cyclotron, and bubble chamber experiments discovered a veritable “zoo” of hadrons, exemplified by a 1964 table of particles in Figure 4.5. While all appeared elementary, several had surprisingly similar properties such as mass and spin, and could also be grouped into invariant subspaces of the isospin group.
In 1961, Murray Gell-Mann and Yuval Ne’eman independently realized that the new hadrons could elegantly fit into representations of a larger symmetry group, [78, 79]. Gell-Mann and George Zweig in 1964 then independently showed that this could be explained physically by hadrons being composed of combinations of three fundamental particles, named the “up”, “down”, and “strange quarks”, with the former two carrying isospin up and down, respectively [80, 81]. Gell-Mann named this model the “eightfold way” (since ) and was awarded the Nobel Prize in 1969 for this work.
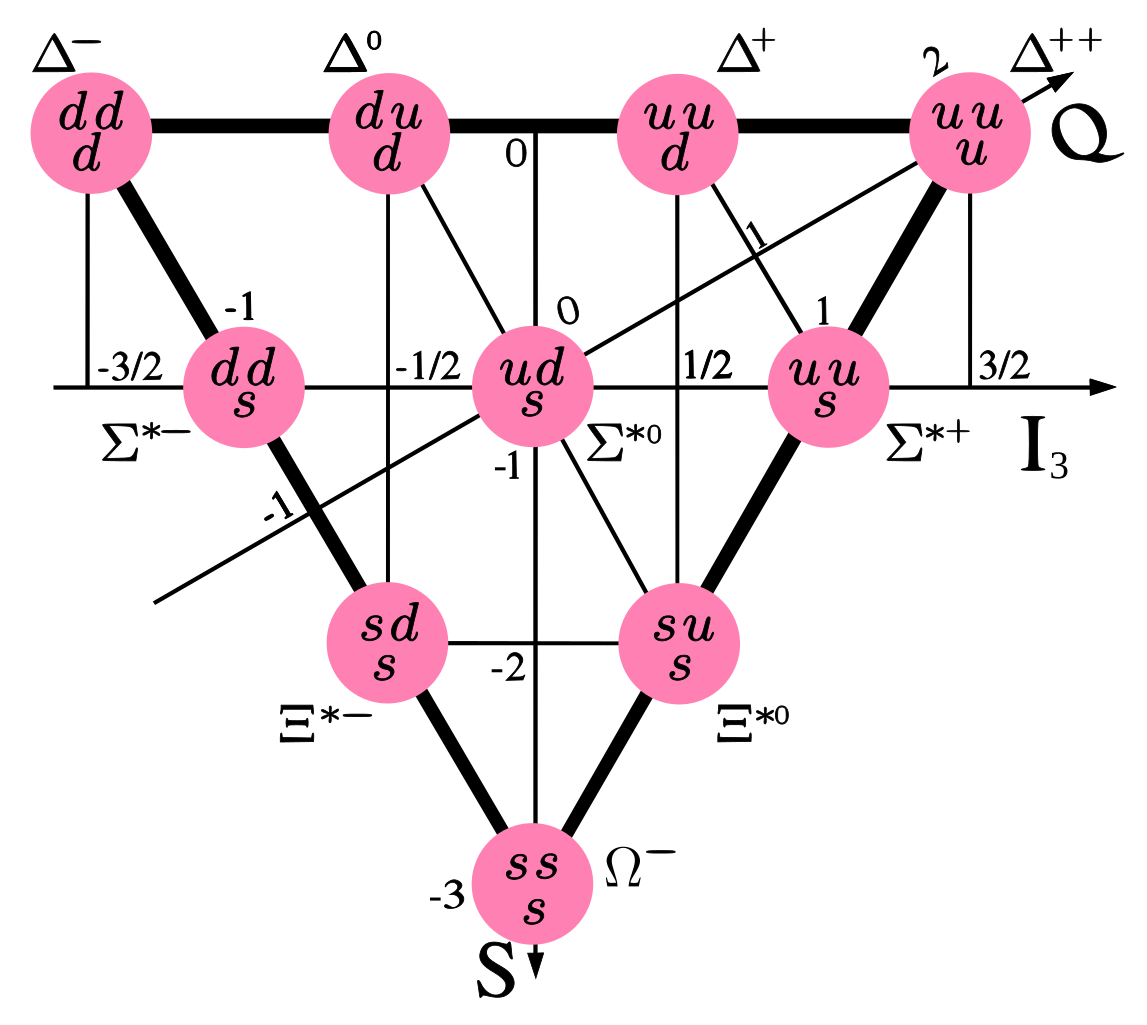
Examples of baryons (three-quark hadrons) in the octet and decuplet (dimension 8 and 10, respectively) representations of are shown in Figure 4.6, sorted by their isospin along the “z” axis ( # of up quarks - # of down quarks) and strangeness ( # of strange quarks). Note that this symmetry is only approximate; it is broken by the different masses of the quarks. However, their significantly smaller masses compared to mean it remains a useful symmetry for categorizing hadrons. On the other hand, broader “symmetries” such as through including the heavier charm, bottom and top quarks are broken so heavily by their higher masses that they are not helpful for characterizing the heavier hadrons.
This fourth “charm” quark was notably predicted by Sheldon Glashow, John Iliopoulos, and Luciano Maiani in 1970 to explain the observed suppression of -boson-mediated flavor-changing neutral currents [83] (and also to match the number of known leptons at the time). This, and the quark model as a whole, was famously validated by the discovery of a charm-anti-charm bound state, named the meson, simultaneously by Burton Richter’s team at the Stanford Linear Accelerator Center (SLAC) and Samuel Ting’s team at Brookhaven National Laboratory in 1974 [84, 85], both of whom received the Nobel Prize in 1976.
A year before this, Makoto Kobayashi and Toshihide Maskawa had proposed the existence of a third generation of quarks to explain the observed CP-violation in weak interactions [86]. This proposal gained more traction after the discovery, as well as the discovery of a third-generation lepton, the , by Martin Lewis Perl’s team in electron-positron collisions at SLAC between 1973 and 1977 [87].
In the end, both third generation quarks were discovered at the Fermi National Accelerator Laboratory (Fermilab): first the bottom quark in 1977 by Leon Lederman’s team on the E288 experiment [88]; and then, much later, the top quark in 1995 by the CDF and DØ experiments at the Tevatron [89, 90]. The bottom quark was discovered indirectly, as with the charm quark, through the observation of a bottom quark-antiquark bound state called bottomium, or the meson, in proton-nucleon collisions.
The top quark, on the other hand, is highly unique because of its high mass, and it decays too quickly to form bound states. Hence, it is the only quark to have been observed “directly”, through its decays to a boson and a bottom quark. It is the heaviest known elementary particle, which is why its discovery required the 1 center-of-mass energy proton-antiproton collisions of the Tevatron. The unique nature of the heavy quarks leads to a rich phenomenology at high energy colliders such as the LHC, particularly in the context of the jets they form (Section 4.1.4).
4.1.3 The parton model
Some physicists, including Gell-Mann himself, initially believed quarks not to be real particles but simply mathematical conveniences to describe hadrons. It was only through deep inelastic scattering (DIS) experiments in the 1960s and 70s at SLAC — in which high energy electrons were shot at protons (in the form of hydrogen) to probe their inner structure — that it was confirmed that protons are indeed not point-like particles.
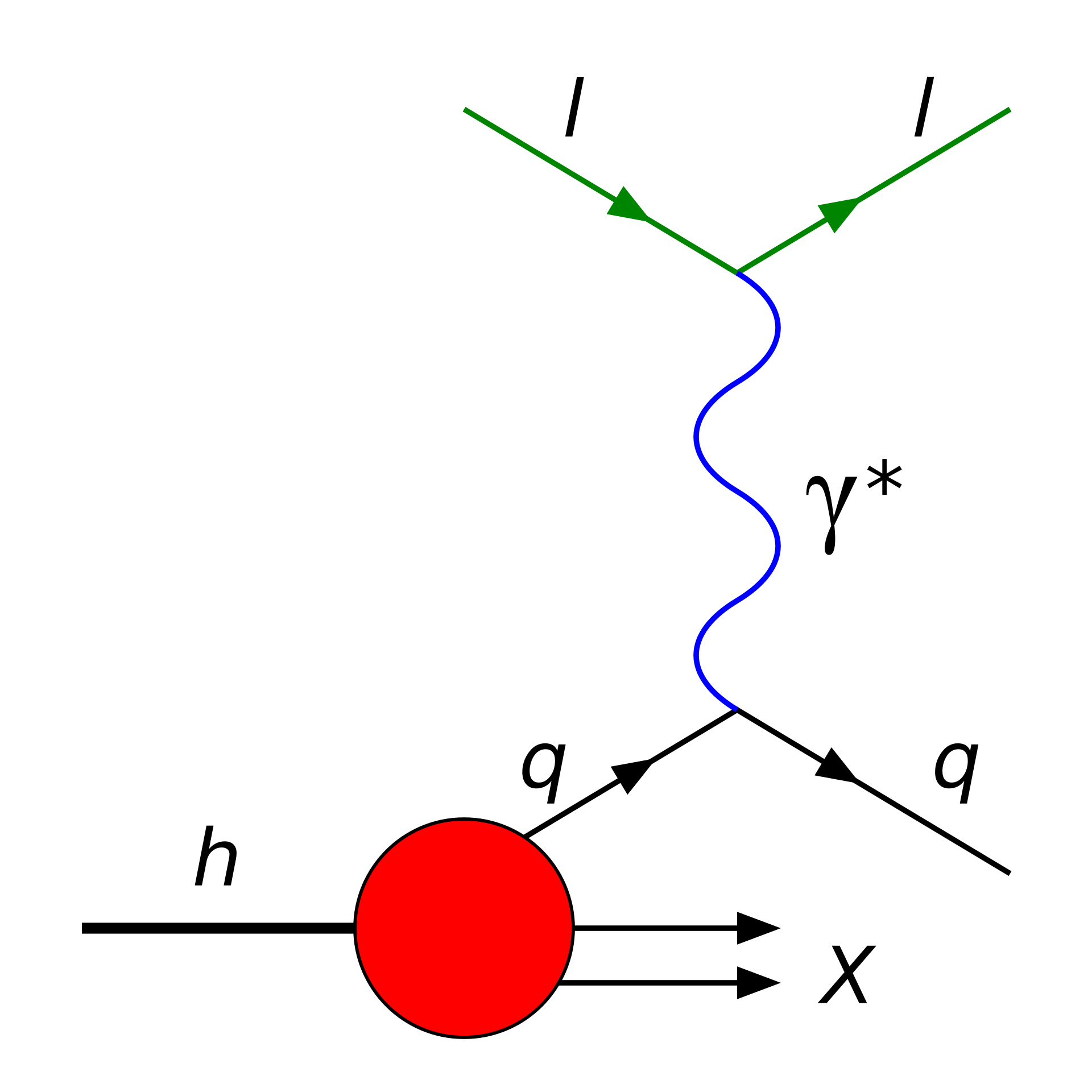
To explain this behavior, Richard Feynman and others proposed the parton model of the proton (and other hadrons). In this, protons are composed of point-like particles called partons that are what actually interact with the electrons in DIS, as illustrated in Figure 4.7. Though initially partons were abstract entities, we now identify them as the quarks and gluons of QCD. At the energies required for DIS (and modern hadron colliders), the “partonic” cross-section of electron-parton scattering (or parton-parton scattering) () can be calculated using standard perturbation theory and Feynman diagrams.
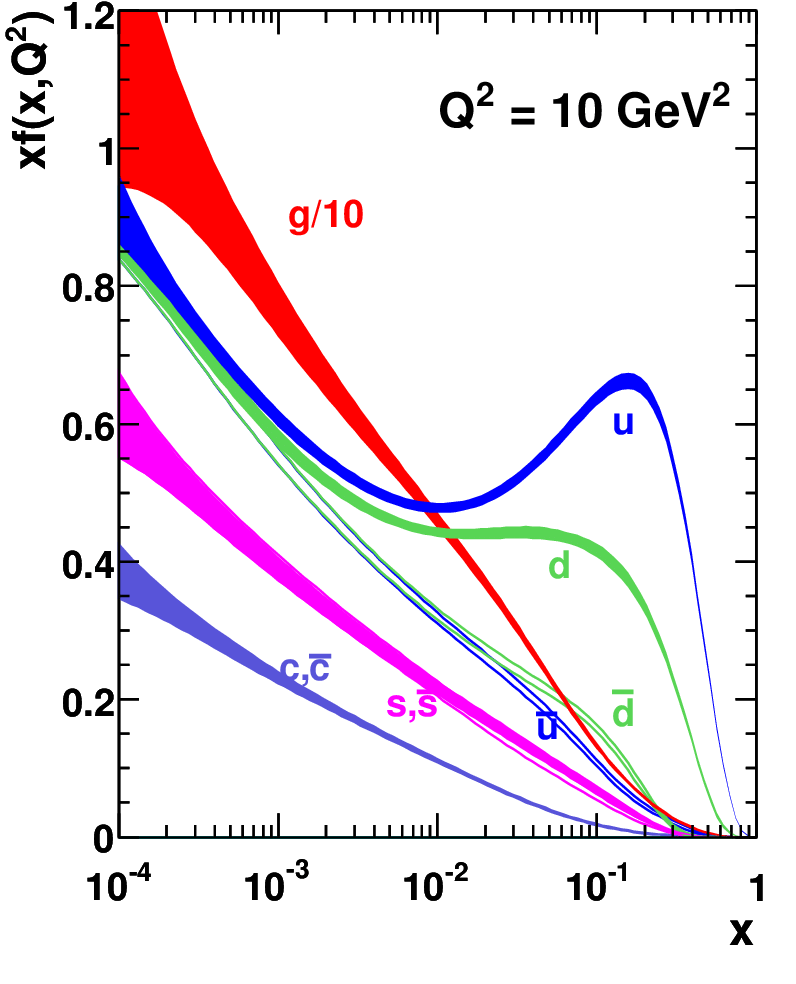
To then derive the total “hadronic” electron-proton cross-section, we must integrate over all possible electron-parton interactions, weighted by the probability of finding a parton carrying a fraction of the proton’s momentum at an energy scale . This is described by the parton distribution functions (PDFs) , where represents the type of parton. PDFs cannot be calculated perturbatively and must be determined from experimental data. Examples for the proton at are shown in Figure 4.8; observe that the up and down quarks — called the valence or “real” quarks — dominate at high , while at lower there are gluons as well as other sea (i.e., virtual) quarks.
The overall hadronic cross-section for DIS is thus:
|
| (4.2) |
where is the scale used for renormalization when calculating the partonic cross-sections. The separation of the perturbative and nonperturbative parts of the cross-section is called factorization, and the fact that this is possible is proved in the factorization theorem [91].
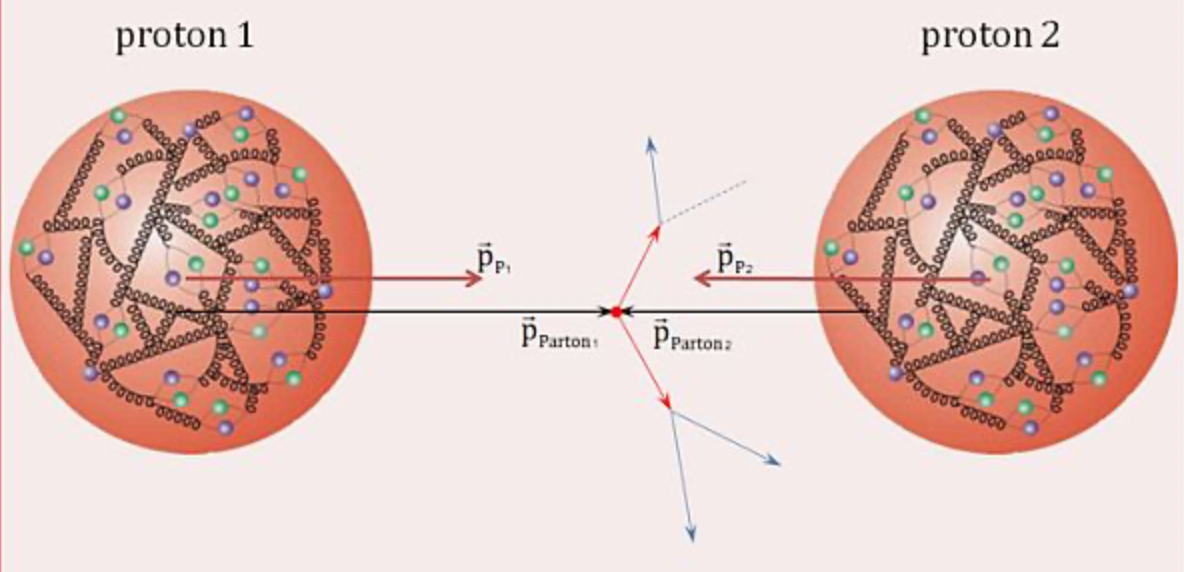
As also illustrated in Figure 4.7, high energy hadron-hadron collisions such as those at the LHC involve a similar, but more complicated, interaction. The corresponding cross-section involves integrating over two partons’ momenta (one each from the two colliding hadrons):
|
| (4.3) |
This is known as the “master formula” for cross-sections at the LHC.3 PDFs are generally measured via DIS at electron-proton colliders, and are then crucial inputs to the above equation for hadron colliders. There is also hope of deriving these through lattice QCD simulations.
The partonic cross section
The partonic cross-section is an important theoretical input for measurements at high energy colliders. The dependence on is perhaps surprising; however, it represents the fact that is calculated perturbatively: the dependence only appears in the highest order term of the expansion. Indeed, this scale dependence would disappear at infinite order in perturbation theory. While it may seem a nuisance, in fact, it provides a convenient handle to estimate the uncertainties on our theoretical predictions by simply varying and .4
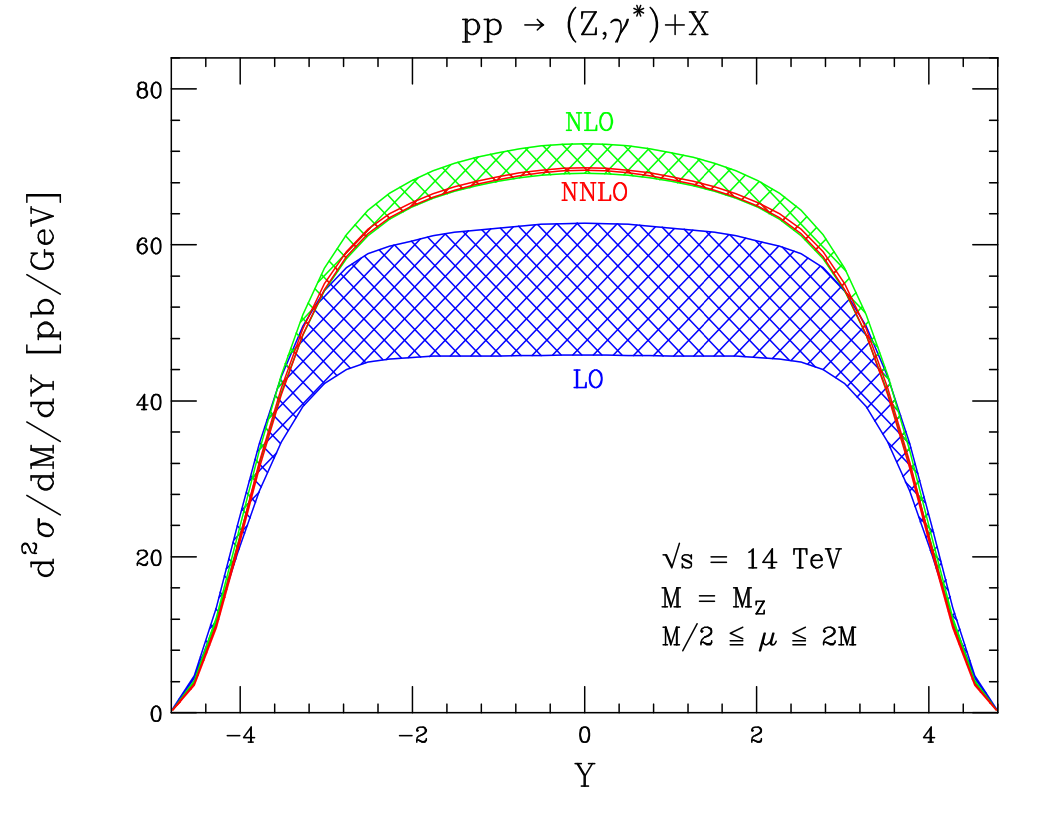
One important feature to keep in mind regarding the perturbative calculations for hadron colliders is that the leading order (LO) predictions are often a factor of off the higher order next-to-LO (NLO) and next-to-NLO (NNLO) calculations. This is exemplified in the predictions for Z boson production at the LHC, shown in Figure 4.9. The reason for this, despite being reasonably small () at the scale for this process , is simply that the corrections have large coefficients [11]. This is why measurements at the LHC relying on LO simulations often multiply the cross-section with an NLO / LO “K-factor”.
Practically, matrix elements are first calculated as a function of the input and output “hard particle” momenta, after which event generator programs such as MadGraph [97] use Monte Carlo (MC) methods to sample events appropriately from the overall phase space. NLO and NNLO calculations are more complicated and often involve weighting events negatively to represent subtractions at higher orders [98].
Parton evolution
Each parton has a certain probability of radiating another quark or gluon, with a fraction of the original parton’s momentum, . These are called parton splitting functions, , depicted in Figure 4.10, and can be calculated perturbatively in QCD (see e.g. Ref. [11]). They are then further convolved with PDFs to derive their evolution with the energy scale:
|
| (4.4) |
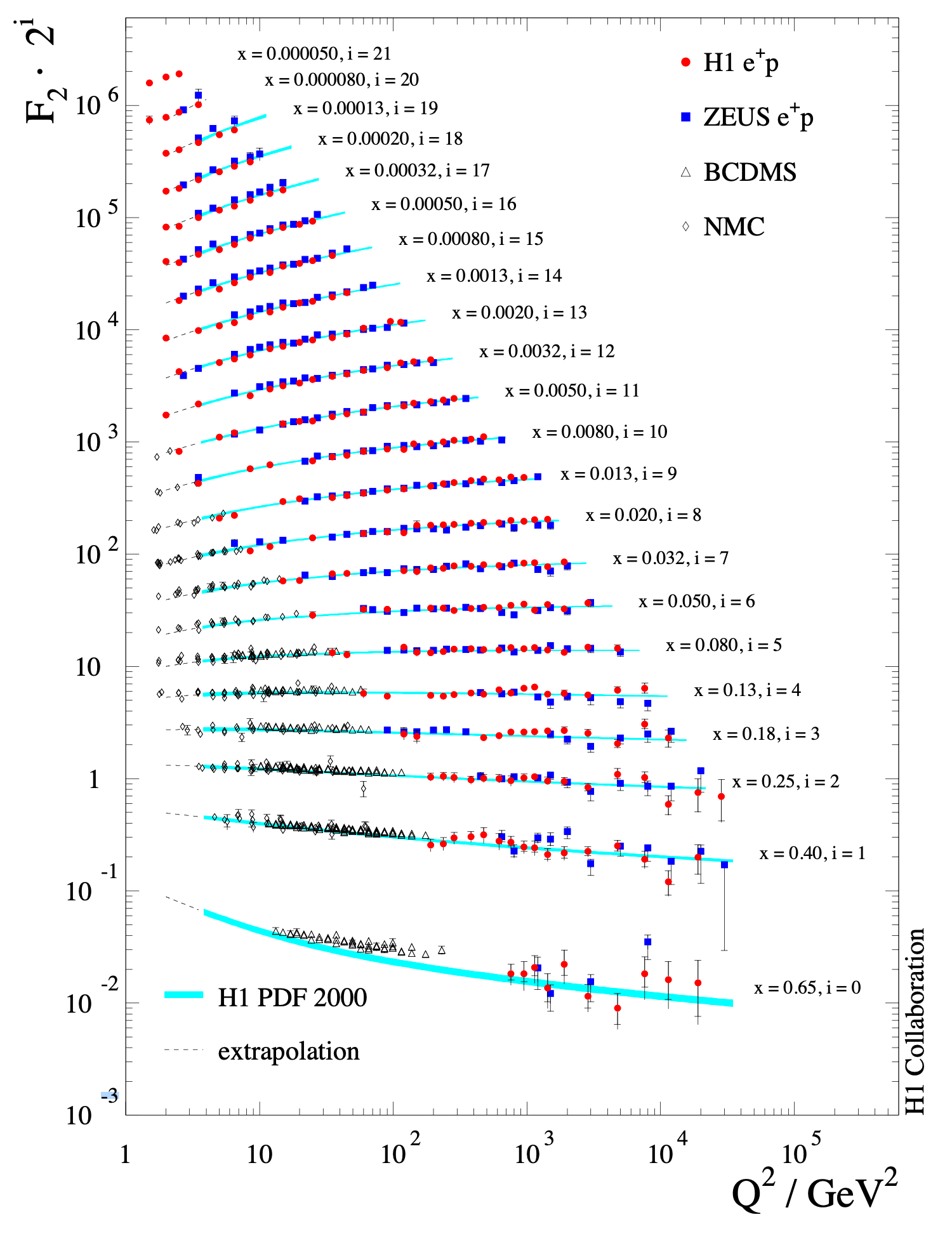
Equations 4.4 are called the Dokshitzer-Gribov-Lipatov-Altarelli-Parisi (DGLAP) evolution equations, after five physicists who developed them in the 1970s, and are analogous to the renormalization group flows of coupling constants. The dependence of the PDFs on the energy scale has been confirmed in DIS experiments, which are then also used to fit the parameters of the PDFs, as shown in Figure 4.11.
4.1.4 Jets
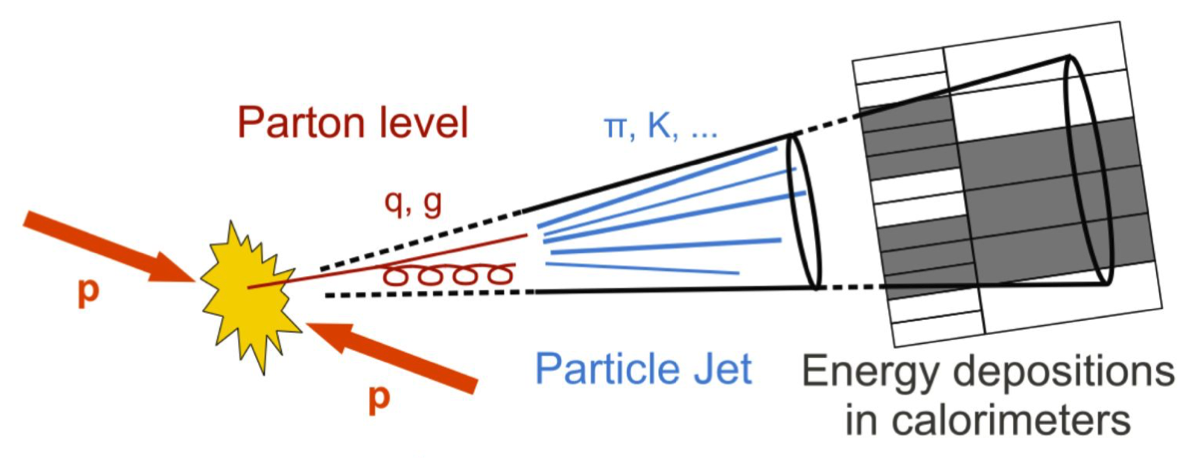
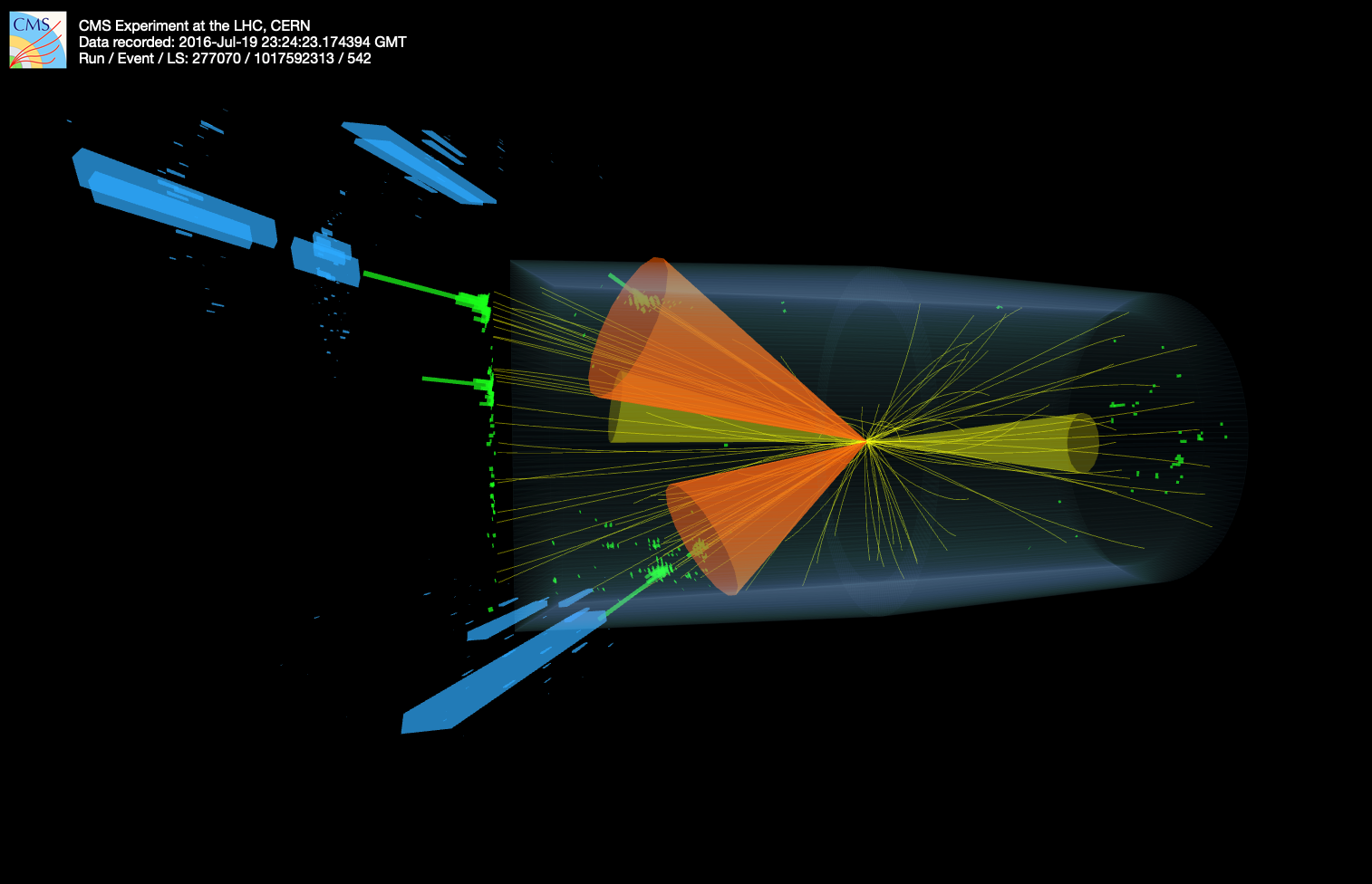
As one may infer from the DGLAP equations (Eq. 4.4), when high energy partons are produced at a collider, they will probabilistically radiate further and further partons — called parton showering — until they approach the confinement scale and start forming bound hadrons — called hadronization. For sufficiently high energy initial partons, the resulting hadrons will appear as a collimated spray of particles in the detector, called a jet (Figures 4.12 and 4.13).
Since quarks and gluons are never observed in isolation, their production can only be inferred by understanding the jets they form. Moreover, at a hadron collider, the high-energy hadrons continuously radiate partons before and after the collision as well, with the resulting jets referred to as initial and final state radiation (ISR and FSR), respectively. Such jets are by far the most prevalent outputs of collisions at the LHC and, hence, represent a significant background in many measurements and searches, particularly those searching for hadronic final states.
Parton showering
Jets can be understood and modeled by factorizing the dynamics. As above, the parton scattering cross section (referred to as the hard process and calculated perturbatively) is separated from the PDFs (measured from data) and their evolution (DGLAP equations). This evolution is what produces the showering, and is modeled by numerically iterating through (or, equivalently, through time) and randomly emitting new partons according to the splitting functions via MC sampling.
There are several subtleties involved in this process which numerical parton shower generators, such as pythia [105], herwig [106], and sherpa [107] must account for. First, the probability of gluon emission diverges in the soft — i.e., low gluon energy — and collinear — small gluon angle with the parent parton — limits. Physically, this can be interpreted as the limit of our experimental resolution: at a certain point we cannot resolve two close-by or detect arbitrarily soft particles.
These are known as the infrared and collinear (IRC) divergences, respectively, and are typically regulated by introducing cut-off energies and angles for emissions (below which we can reasonably argue that perturbation theory is anyway invalid). These divergences also mean that when analyzing jets in experimental data, care must be taken in defining observables to be IRC-safe, meaning that jet clustering algorithms and physical properties derived therein should not be sensitive to arbitrarily soft or collinear emissions.
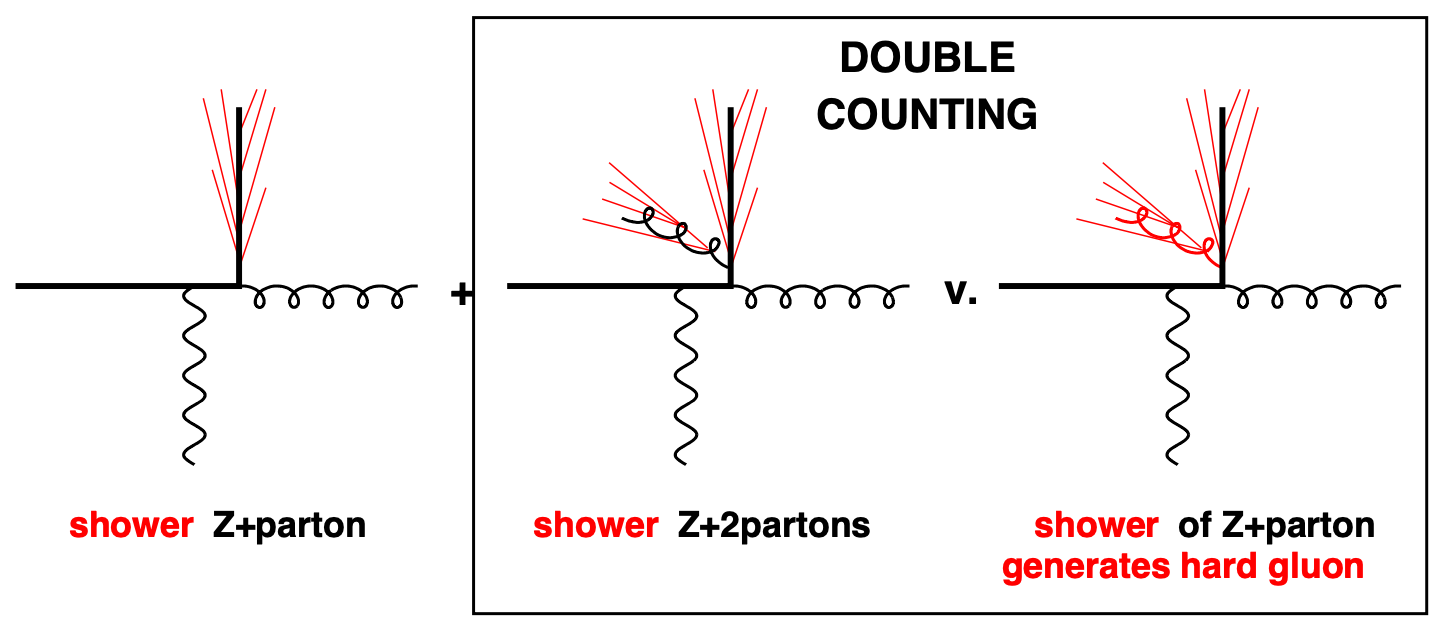
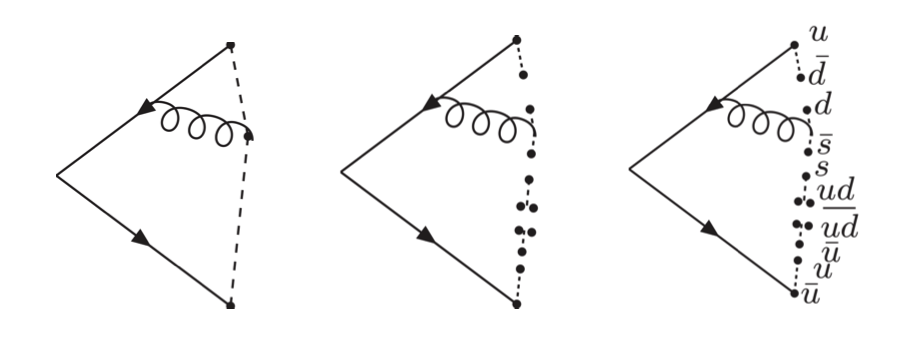
Another issue is that a naive combination of the hard matrix element and subsequent parton shower calculations may lead to double-counting of emissions, as illustrated in Figure 4.14. This necessitates a careful “matching procedure”, such as the most common MLM scheme [108], which defines cut-off energy and angular scales to separate the matrix element and parton shower phase spaces. Other considerations include preserving unitarity, color coherence and color flow, and differences between ISR and FSR (see e.g. Refs. [109, 110]).
Hadronization
The final element of the factorized process is hadronization, once the parton shower approaches the confinement scale. This is a completely nonperturbative process and, hence, like PDFs, we must rely on numerical simulations and experimental measurements.
Lattice QCD simulations, such as those shown in Figure 4.4, indicate that in the low energy limit, the effective potential between quarks increases linearly with distance, resembling string tension:
|
| (4.5) |
where is the string tension coefficient. In fact, this analogy can be extended further: above a certain energy, the string appears to “snap”, in the sense that it becomes possible and energetically more favorable to produce a quark-antiquark pair.
This analogy the basis of the Lund string model of hadronization [111], illustrated in Figure 4.15. The strong force between the final state partons is modeled as a series of strings stretched between them that probabilistically break into new partons. Other models are based on clustering partons into color-neutral combinations [106].