Chapter 4
The Standard Model
Before I came here, I was confused about this subject. Having listened to your lecture, I am still confused. But on a higher level. — Enrico Fermi1
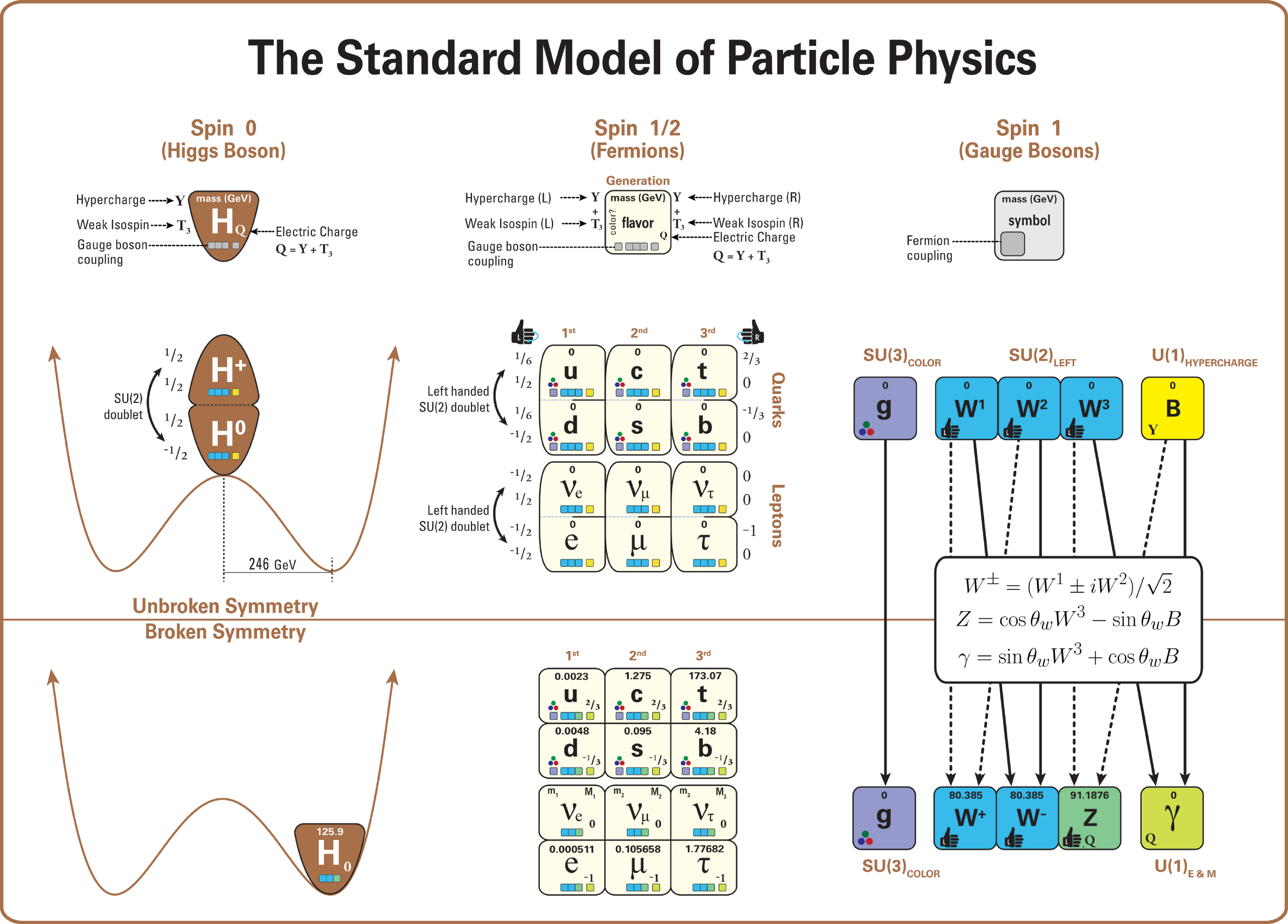
We are now ready to describe the standard model (SM)! It is a renormalizable, quantum Yang-Mills theory, and is illustrated nicely in Figure 4.1. Before electroweak symmetry breaking (EWSB) — a form of spontaneous symmetry breaking (SSB) — it possessed the gauge symmetry , with , , and standing for color, left, and hypercharge, respectively. These three groups correspond to the strong, weak, and electromagnetic forces, with eight, three, and one generators or gauge bosons, respectively. The relative strengths of each interaction, as well as gravity’s, are shown in Table 4.1, based on the equivalent of the fine structure constant of each force, , where is the respective coupling constant.
The SM contains six fermions charged and uncharged under the symmetry each, called the “quarks” and “leptons”, respectively. The left-handed fermions live as pairs in doublets, while the right-handed fermions in singlets. The six types of fermions are referred to as different “flavors”, grouped into three generations as in Figure 4.1.
The SM also contains a complex scalar -doublet called the Higgs field, which is associated with EWSB. As shown in Figure 4.1, it initially is at the center of a “sombrero” potential because of which, before EWSB, the gauge bosons, fermions, and the Higgs field are all massless.
EWSB is hypothesized to have occurred during the electroweak epoch (between around and after the big bang), where the global symmetry broke to the of QED. Through this, the Higgs field obtained a non-zero vacuum expectation value (VEV), imbuing all the fermions, three of the gauge bosons, and the Higgs boson with mass — a process referred to as the Higgs mechanism. The outcome is the state of the universe and physics as we know it.
Of course, as outlined in the introduction, this picture does not explain myriad phenomena in fundamental physics, including dark matter, dark energy, baryon asymmetry, and neutrino masses. This is why it is crucial to test the SM as rigorously and in as broad a phase space as possible, in order to identify any cracks that may point to new physics.
| Force | Strength |
| Electromagnetic | |
| Weak | |
| Strong | |
| Gravity |
In this chapter, we will briefly walk through different areas of the SM. Having discussed QED in Chapter 3.5, we now describe the remaining two fundamental interactions: quantum chromodynamics (QCD) in Section 4.1; and weak interactions and electroweak unification in Section 4.2. We conclude with a discussion of phenomena that the SM cannot explain, and what my lie beyond, in Section 4.3.
4.1.1 Asymptotic freedom and confinement
4.1.2 Quarks and the eightfold way
4.1.3 The parton model
4.1.4 Jets
4.2 Electroweak interactions
4.2.1 Weak interactions
4.2.2 Before electroweak symmetry breaking
4.2.3 Electroweak symmetry breaking
4.2.4 Fermion masses and flavor
4.3 Beyond the Standard Model [Coming Soon!]
1Also an accurate representation of my understanding of the SM before and after my PhD.