7.2 Equivariant neural networks
ANNs and DL have shown remarkable success in a wide range of computer vision and NLP tasks, motivating applications to the physical sciences. However, as highlighted in the previous section, the power of DL models is often derived from architectures tuned to the inductive biases of their domains.
A unique feature of physical data is its inherent physical symmetries (see Chapter 2), such as with respect to and Lorentz-transformations for molecules and high-energy collisions, respectively. It is hence desirable to develop NN architectures that themselves are intrinsically equivariant to the associated transformations, which can thereby be more data efficient, more easily interpretable, and perhaps ultimately more successful [231].
We have already encountered some forms of equivariance: to translations in CNNs and to permutations in GNNs. More recently, there has been work on building equivariance to a broader set of transformations, such as the symmetries mentioned above, which will be the focus of this section.
7.2.1 Equivariance
Let us first introduce precisely what we mean by “equivariance”, adapting a definition from Refs. [232–235].
Definition 7.2.1. A feature map is considered equivariant to a group of transformations if and some representation there exists a representation satisfying
|
| (7.2.1) |
i.e. the group operation commutes with the map (and therefore is an intertwiner). In this context, generally represents a NN layer. Another way to think about this is that each transformation by a group element on the input must correspond to a transformation by the same group element in the feature space (but with potentially different representations and ).
Definition 7.2.2. Invariance is the particular case where is the trivial representation ( ), wherein transformations on do not affect features at all.
While for many tasks, such as classification, invariance of the outputs is sufficient, Refs. [233, 234] argue that equivariance is more desirable at least in the intermediate layers, as it allows the network to learn useful information about the transformation itself.
So far, we have discussed CNNs and GNNs / transformers, which are equivariant to the group (translations in dimensions) and invariant to the group (permutations of objects), respectively. Next, we discuss the extension to broader symmetry groups.
7.2.2 Steerable CNNs for -equivariance
We first describe the generalization of the translational invariance of CNNs to equivariance to not only translations, but rotations and reflections in 2D as well; i.e, the group. We make use of a general procedure, based on Refs. [232, 233], for extending 2D translational invariance () to equivariance to a group , where is the semi-direct product and is a subgroup of , meaning we can induce representations of , , from .1 For , in particular, , the group of distance-preserving transformations in 2D; i.e., rotations and reflections.
The key idea in developing a -equivariant layer is to first find the set of maps which satisfy Eq. 7.2.1 for an element :
|
| (7.2.2) |
where and are reps of . After this, Eq. 7.2.1 can be automatically satisfied using
|
| (7.2.3) |
where for some 2D translation .
Since Eq. 7.2.2 is linear in , we want a complete linear basis of functions that satisfy it. We can obtain this by restricting the convolutional filters of a standard CNN to circular harmonics [234]:2
|
| (7.2.4) |
where the radial component and the filter phase are learnable parameters. We can see that , these filters form a complete basis and satisfy Eq. 7.2.2 under convolutions () with an image rotated by :
|
| (7.2.5) |
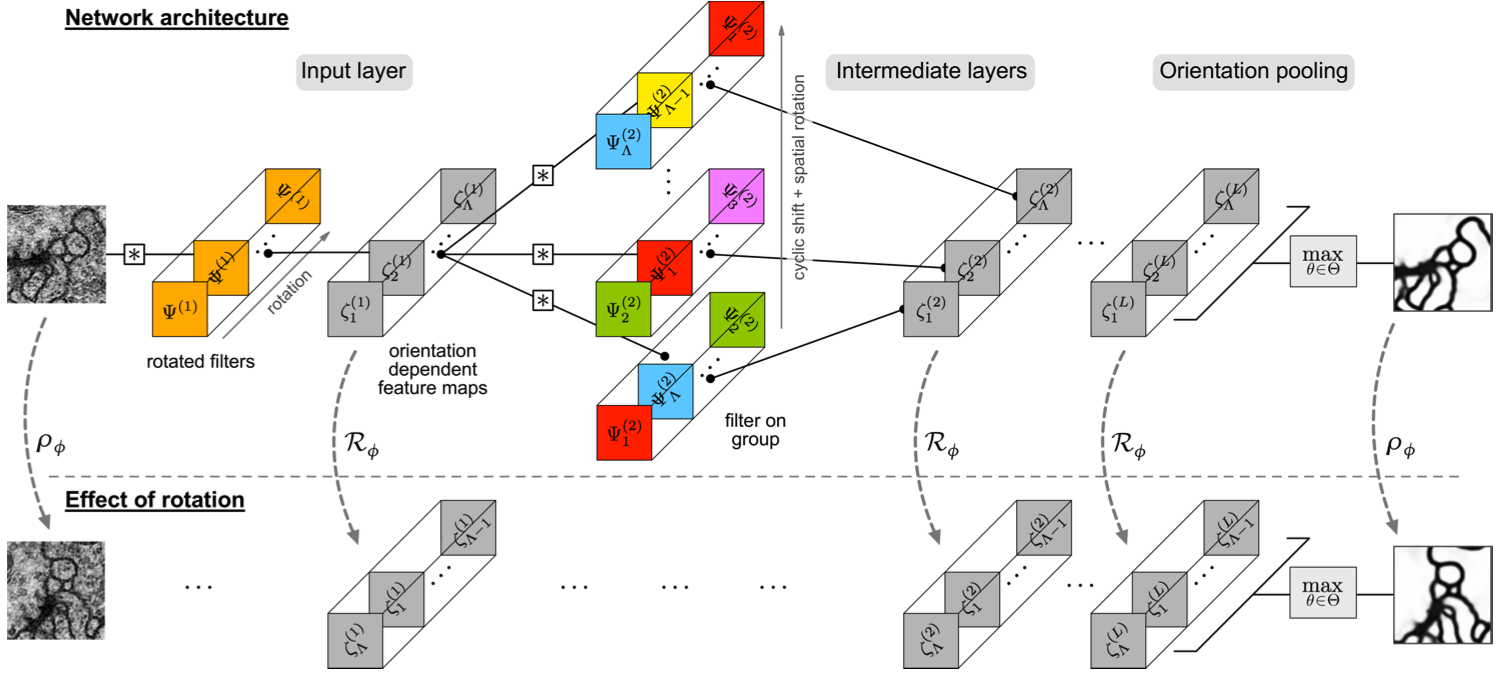
Here we took to be the fundamental rep acting on the image and to be any one of the infinite complex reps. After discretizing these filters Ref. [234] demonstrates significant improvement in classification of rotated images compared to SOTA CNNs. Such networks are generally referred to as “Steerable CNNs”, and, in practice, are implemented using a finite set of such circular harmonic filters, with (and possibly their reflections), which are then pooled in a rotationally-invariant manner, as illustrated in Figure 7.8.
7.2.3 Tensor-field networks for -equivariance
Steerable CNNs have been extended to -equivariance — translations, rotations, and reflections in 3D — as well [236]. However, we will discuss a slightly different approach, applied to point-cloud data. This approach uses “Fourier decompositions” of the input, feature, and output spaces into irreducible representations (irreps) of the symmetry group, and is referred to as a “tensor-field network” [231]. In addition to their aforementioned applications to HEP, point clouds are also extremely useful representations of physical objects such as molecules and crystals, both of which are inherently invariant.
In the approach of Ref. [231], the input and intermediate network layers take the set of coordinates and features for each point in the point cloud and map them to the same set of coordinates with new learned features (), with an equivariant again having to satisfy Eq. 7.2.1. If necessary, the features are aggregated at the end across all points to produce the output. Translation equivariance is achieved directly by requiring to only consider distances between points and (a global translation will not affect these).
For rotation equivariance, first the feature vectors are decomposed according to how they transform under irreps of — scalars, vectors or higher order tensors (the coordinates already transform as vectors in under the fundamental rep):
|
| (7.2.6) |
where the sum is performed over irreps (with dimension ) and are the multiplicities. Thus, each point’s features and coordinates have the corresponding decomposition:
|
| (7.2.7) |
where the are tensors which transform under the irrep. Similar to steerable CNNs, each of these tensors are individually acted upon by generalized convolutional filters with the form , where is a learned radial function, are the spherical harmonic tensors, and the set corresponds to the set of desired irreps in feature space. The spherical harmonics are directly analogous to using circular harmonics for (except they have dimension ) and by the same argument they satisfy Eq. 7.2.1. This convolution effectively produces a tensor product representation of , which is then decomposed via Clebsch-Gordan (CG) decomposition into irreps again.
A useful pedagogical example is of a network taking as input a collection of point masses and outputting the inertia tensor. The input features are the masses of each point, which are scalars under , and the inertia tensor transforms as the representation, so we define this network to be of the type .
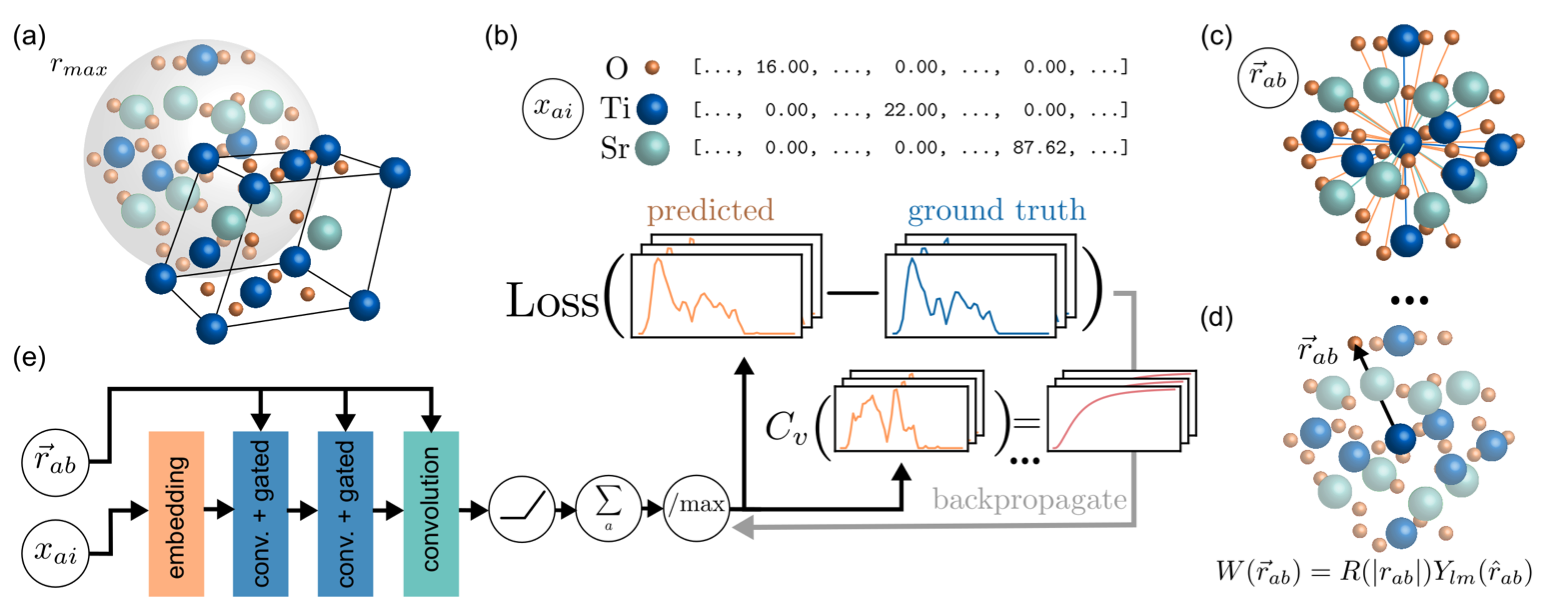
Some interesting and successful applications include classifying molecules [237], predicting protein complex structures [238], and predicting the phonon density of states (DoS) in crystals [53]. A schematic of the architecture used for the latter is shown in Figure 7.9. Different crystals are represented geometrically as point clouds in , with individual atoms labeled via feature vectors using mass weighted one-hot encoding. After a series of convolution layers the features are summed over all points to predict 51 scalars comprising the phonon DoS.
7.2.4 Lorentz-group-equivariant networks
Recently there has been some success in creating Lorentz-group-equivariant networks, which are desirable for DL applications to high energy data. The Lorentz group comprises the set of linear transformations between inertial frames with coincident origins. Henceforth, we restrict ourselves to the special orthochronous Lorentz group , which consists of all Lorentz transformations that preserve the orientation and direction of time. Equivariance to such transformations is a fundamental symmetry of the data collected out of high-energy particle collisions.
To our knowledge, there has been no generalization of steerable CNNs to the Lorentz group; however, Refs. [54, 239–241] propose an alternative, completely Fourier-based approach, again acting on point clouds, that shares some similarities with the -equivariant network discussed above.
The general method is to:
- 1.
- Decompose the input space into irreps of the group.
- 2.
- Apply an equivariant mapping (satisfying Eq. 7.2.1) to the feature space.
- 3.
- Take tensor products of the irreps and CG-decompose them again into irreps.
- 4.
- Repeat steps 2–3 until the output layer.
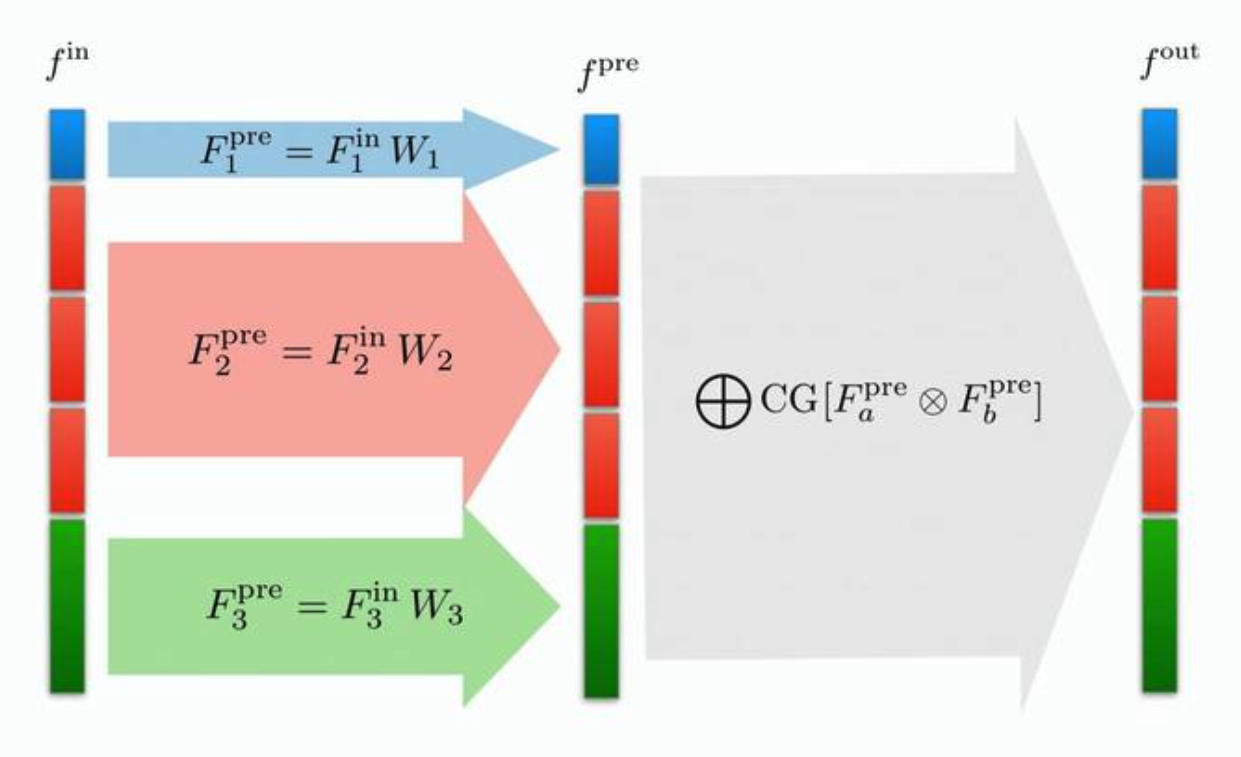
The crucial difference between this and the previous networks is that the mapping is no longer via convolutional filters; instead, it is chosen to be a simple linear aggregation across the nodes of the point clouds. Recall from Definition 7.2.1 that equivariant maps must be intertwiners between input and output representations, which, according to Schur’s Lemma, imposes strong restrictions on both the form of a linear and its output . Namely: the outputs and inputs must have the same irrep decomposition (though the multiplicities are allowed to vary, akin to increasing/decreasing the “channels” in an image) and must be a direct sum of learned matrices acting individually on each irrep. The transformation between and in Figure 7.10 illustrates such a mapping.
To inject non-linearities into the network, Ref. [54] proposes to take tensor products between each pair of irreps after the mapping, and then perform a CG decomposition.3 Another freedom available to us is acting with arbitrary learned functions on any scalar irreps that result from the decomposition, since they are, by definition, Lorentz-invariants.
One successful application of this network has been to jet tagging: Ref. [54] successfully applied this “Lorentz-group network” (LGN) to top-quark identification, demonstrating a high (92.9%) accuracy, though they were unable to match the then-SOTA (93.8% using the ParticleNet GNN [230]).
Finally, we note that overall this is, in fact, a very general approach: applicable to any symmetry group. This includes the aforementioned and groups as well as potentially more exotic groups such as or which also arise in physics. The only group-dependent operations in such a network are the decompositions into irreps which can readily be calculated for any group (as opposed to steerable CNNs where one needs to derive group equivariant kernels/convolutional filters).
Summary
We reviewed three approaches to creating neural networks that are equivariant to physical symmetry groups: by extending the translation-equivariant convolutions in CNNs to more general symmetries with appropriately defined learnable filters as in Refs. [232, 243, 244], by operating in the Fourier space of the group [54], and a combination thereof [231]. Such networks are highly relevant to the physical sciences, where datasets often possess intrinsic symmetries, and, as demonstrated in some example tasks, they are promising alternatives and improvements to standard non-equivariant DL approaches. In particular, Lorentz-equivariant networks have shown promise in jet classification, a key task in HEP. In Chapter 16, we will discuss the extension of these ideas to the first Lorentz-equivariant autoencoder for jets, with applications to data compression, anomaly detection, and potentially fast simulations as well.