7.3 Autoencoders and generative models

7.3.1 Autoencoders and anomaly detection

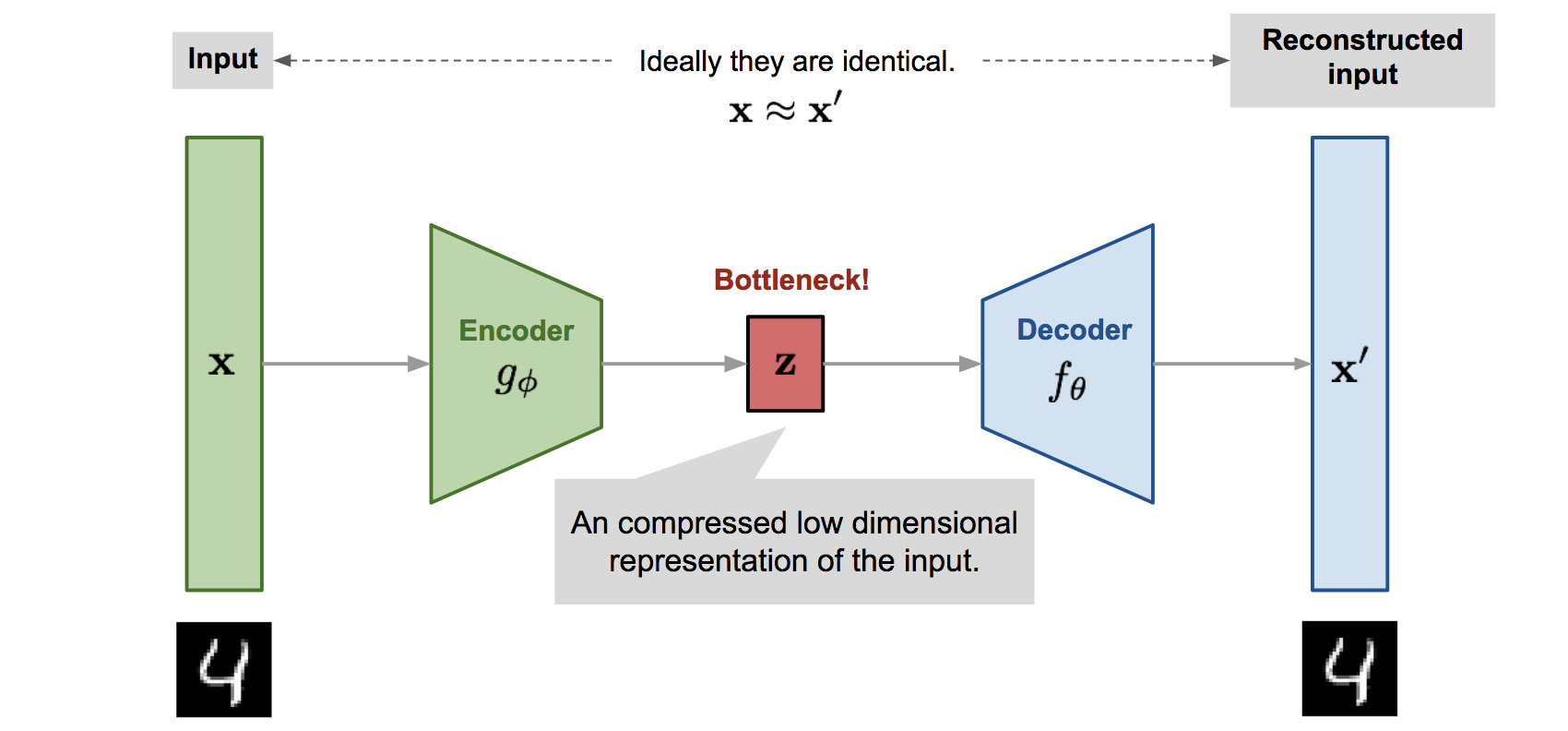
In this final section, we discuss two paradigms of unsupervised learning relevant to this dissertation: autoencoders (AEs) and generative models. AEs are NN architectures composed of an encoder network, which maps the input into a typically lower dimensional latent space — called a “bottleneck” — and a decoder, which attempts to reconstruct the original input from the latent features (Figure 7.11). The bottleneck encourages AEs to learn a compressed representation of data that captures salient properties [245], which can be valuable in HEP for compressing the significant volumes of data collected at the LHC [246].

The learned representation can also be exploited for later downstream tasks, such as anomaly detection, where an autoencoder is trained to reconstruct data considered “background” to our signal, with the expectation that it will reconstruct the signal worse than the background. Thus, examining the reconstruction loss of a trained autoencoder may allow the identification of anomalous data. This can be an advantage in searches for new physics, since instead of having to specify a particular signal hypothesis, a broader search can be performed for data incompatible with the background. This approach has been successfully demonstrated in Refs. [247–255]. Two recent exciting examples from CMS include a model-agnostic search for di-jet resonances with Run 2 data [256], which prominently uses AEs for multiple search strategies, and a new AE-based online Level-1 trigger paths implemented in Run 3 [257, 258].

Furthermore, there are many possible variations to the general autoencoder framework for alternative tasks [259, 260], such as variational autoencoders (VAEs) [261], which we discuss in the next section. While there have been some recent efforts at GNN-based autoencoder models [67, 262], in this dissertation, we present the first Lorentz-equivariant autoencoder for jets in Chapter 16. We focus on data compression and anomaly detection but note that our model can be extended to further applications, such as fast simulations in HEP.

7.3.2 Generative models

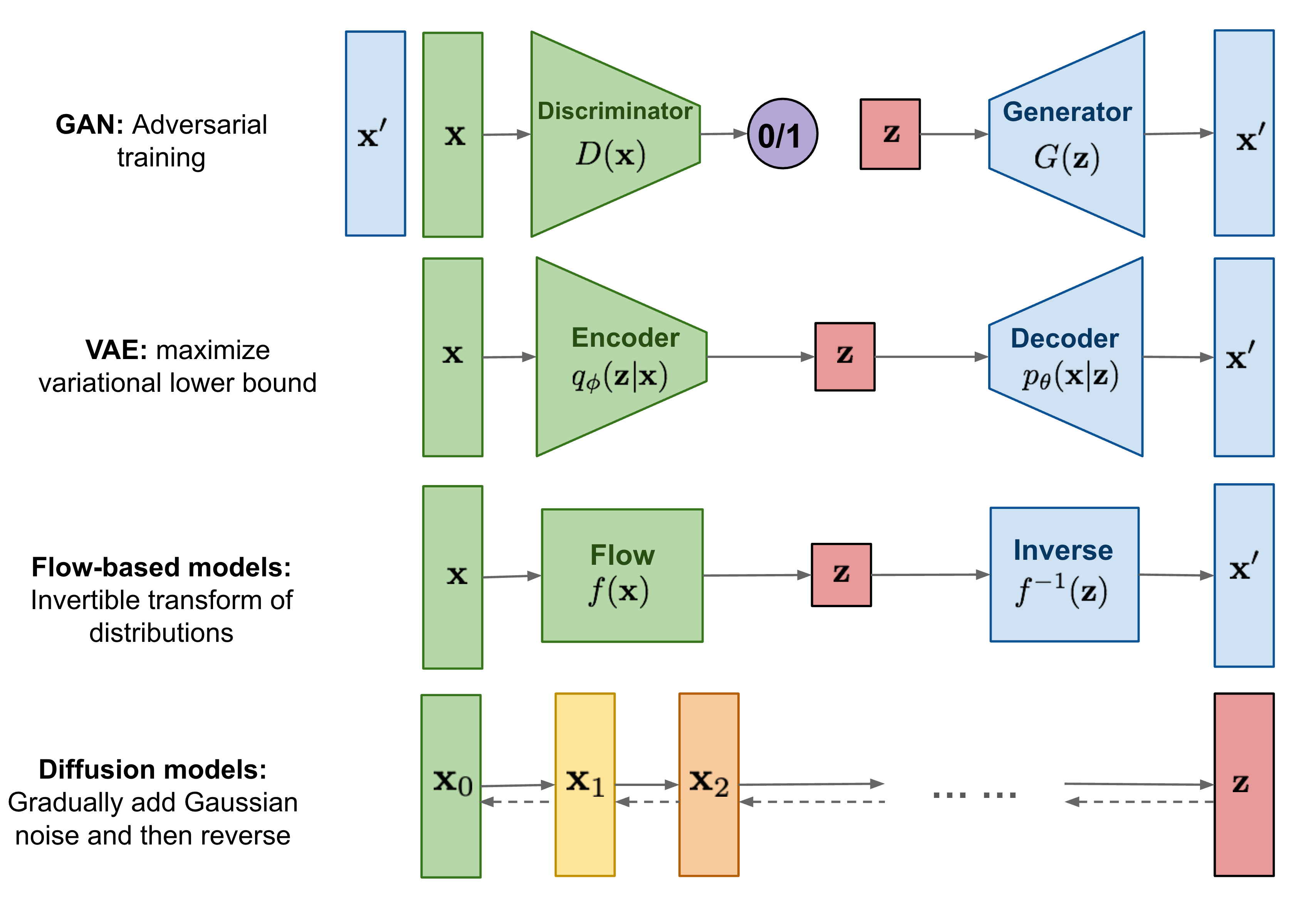
Generative models are a class of statistical models that aim to capture the probability distribution of the data $p(x)$ in order to generate new samples. This is a challenging problem, but one that has seen significant progress in recent years with DL, particularly in computer vision and NLP. We will briefly walk through four popular approaches, illustrated in Figure 7.12, which can be broadly categorized as likelihood-based or implicit models.

Likelihood-based models

Likelihood-based models attempt to directly learn the probability distribution of the data through some form of (approximate) likelihood maximization.⁴ Flow-based models, for example, learn a series of invertible transformations to map a simple base distribution that is easy to sample from, such as a Gaussian, to the complex target data distribution. The most popular of these at the time of writing are “normalizing flows”, which require each transformation to have a tractable Jacobian determinant with which to correctly normalize the result.

Normalizing flows have a number of advantages, such as their simple and intuitive training objective — maximizing the likelihood of each data point — and a tractable likelihood evaluation. These have led to successful applications to density estimation and generation tasks in both computer vision [263, 264] and HEP [265]. However, the constraint of invertible transformations with tractable Jacobians turns out to be extremely restrictive on the model design and expressivity in practice [266, 267], generally resulting in worse performance on high-dimensional data compared to the models we discuss below. Recently, over the last year, a related (in spirit) class of models without the normalization constraint, called “flow-matching” models, have emerged with extremely promising and, in some cases, state-of-the-art (SOTA) results on images [268, 269].

Another example of a likelihood-based model is the variational autoencoder (VAE) [261], which is structurally similar to an AE in that it has an encoder mapping an input data point into a latent representation, and a decoder mapped that back to the original. They key novelty, however, is that the latent space is encouraged through the loss function to follow a well-defined simple distribution to sample from — again, typically, a Gaussian. Explicitly, the VAE loss function is a combination of the reconstruction loss of a standard AE and the Kullback-Leibler divergence between the learned latent distribution and the assumed prior. Together, this can be shown to approximate the evidence lower bound (ELBO) of the true likelihood [261], which is why VAEs are thought of as likelihood-based.

VAEs were one of the early success stories in generative modeling, with a relatively simple implementation, training, and learning objective. However, they again are restrictive, this time due to the strong assumption imposed on the latent space, which actually competes with the reconstruction objective, and which, if incorrect, limits the performance. Indeed, our early studies in HEP showed that the learned latent space of VAEs is manifestly non-Gaussian for jets, leading to suboptimal performance with a Gaussian latent prior [270]. This is why VAEs also generally yield poorer performance than generative adversarial networks (GANs) [271], which we discuss next.

GANs

GANs are a type of implicit generative model. This means they learn to generate samples without directly learning the likelihood of the data. Instead, their loss function is effectively provided by a second neural network, called the discriminator or critic, which tries to distinguish between real and generated samples. The two generator and discriminator networks, with the former aiming to fool the latter, are trained iteratively and adversarially, forming a feedback loop and progressively improving each other. This continues until, ideally, the duo converge to a point where the generator produces samples indistinguishable from the real by the discriminator.

GANs have an interesting game-theoretic interpretation as a minimax game, where the Nash equilibrium, or global optimum, is achieved through minimizing the Jensen-Shannon divergence between the real and generated data distributions [271]. Several variations of GANs have also been proposed, including the Wasserstein-GAN [272], which instead aims to minimize the Wasserstein distance between the two distributions.

Due to the adversarial nature of the training, GANs are notoriously difficult to train [272–275]. However, their formulation poses no restrictions on the form of the generator while providing a powerful loss function and feedback mechanism. When trained successfully, this leads to expressive, flexible, and extremely successful generative models in a wide variety of domains. Indeed, at the time of the work of this dissertation, GANs were the SOTA in computer vision [276–278] and had shown promising signs in HEP as well [229, 279–283]. However, as we highlight below, there had been no successful application of GANs, or indeed any generative model, to point cloud data and GNNs or transformers in HEP.

Score-based diffusion models

Finally, we briefly note the recent development in the past two years of a new class of generative models, called diffusion or score-based models [284, 285]. These models iteratively “denoise” initial Gaussian noise into something resembling samples from the true data distribution; conceptually, this is related to diffusion in physical systems. The breakthrough with these models came from recognizing that, with the right learning objective, this denoising process is in fact equivalent to following the gradient of the log-likelihood function, AKA the score.

Diffusion models allow a likelihood-driven training objective, like flow-based models, but without the restrictive constraints (as the score does not need to be normalized!), thereby offering the flexibility of a GAN along with a far more stable training procedure. This, combined with several innovations in training and inference techniques, has led to diffusion models surpassing GANs in computer vision [286], and showing promising signs over the last year in HEP as well (in part enabled by the work in this dissertation, as we discuss in Chapter 12). However, so far, diffusion models remain computationally expensive, with inference naively requiring up to hundreds of denoising steps, which limits their application to fast simulations. Nevertheless, they are an exciting area for exploration in future work.

7.3.3 Previous work

Note: the following discussion represents the state of the field at the time of our first publications in 2021, to provide context. Since then, the field has evolved significantly, partly due to the work presented in this dissertation, as we discuss in Chapter 12.

Generative modeling in HEP

Past work in generative modeling in HEP exclusively used image-based representations for HEP data. The benefit of images is the ability to employ CNN-based generative models, which have been highly successful on computer vision tasks. References [229, 279–283], for example, build upon CNN-based GANs, and Ref. [287] uses an autoregressive model, to output jet- and detector-data-images.

However, as highlighted in Section 7.1.4, the high sparsity of the images can lead to training difficulties in GANs, while the irregular geometry of the data poses a challenge for CNNs which require uniform matrices. While these challenges can be mitigated to an extent with techniques such as batch normalization [219] and using larger/more regular pixels [281], the approach we develop avoids both issues by generating particle-cloud-representations of the data, which are inherently sparse data structures and completely flexible to the underlying geometry.

Point cloud generative modeling

Prior to this work, point cloud generative approaches had not yet been developed in HEP; however, there had been some work in computer vision, primarily for 3D objects like those from the ShapeNet dataset [288]. As shown in Figure 7.13, ShapeNet comprises point clouds derived by sampling everyday objects in position space, and are thus naively analogous to the particle cloud representations in momentum space we employ for jets. However, as we note next, there are important differences in the inductive biases of the two datasets.

Firstly, jets have physically meaningful low- and high-level features such as particle momentum, total mass of the jet, the number of sub-jets, and $n$-particle energy correlations. These physical observables are how we characterize jets, and hence are important to reproduce correctly for physics analysis applications. Secondly, unlike the conditional distributions of points given a particular ShapeNet object, which are identical and independent, particle distributions within jets are highly correlated, as the particles each originate from a single source. The independence of their constituents also means that ShapeNet-sampled point clouds can be chosen to be of a fixed cardinality, whereas this is not possible for jets, which inherently contain varying numbers of particles due to the stochastic nature of particle production. Indeed, the cardinality is correlated with other jets features such as the jet mass and type.

Baseline models from computer vision

Still, particle clouds and point clouds have similarities insomuch as they represent sets of elements in some physical space, hence we first test existing point cloud GANs as baseline comparisons on JetNet. There are several published generative models in this area; however, the majority exploit inductive biases specific to their respective datasets, such as ShapeNet-based [289–292] and molecular [293–295] point clouds, which are not appropriate for jets. A more detailed discussion, including some experimental results, can be found in Appendix C.1.1.

There do exist some more general-purpose GAN models, namely r-GAN [296], GraphCNN-GAN [297], and TreeGAN [298], and we test these on JetNet. r-GAN uses a fully-connected (FC) network, GraphCNN-GAN uses graph convolutions based on dynamic $k$-nn graphs in intermediate feature spaces, and TreeGAN iteratively up-samples the graphs with information passing from ancestor to descendant nodes. In terms of discriminators, past work has used either an FC or a PointNet [299]-style network. Ref. [300] is the first work to study point cloud discriminator design in detail and finds amongst a number of PointNet and graph convolutional models that PointNet-Mix, which uses both max- and average-pooled features, is the most performant.

In Chapter 10, we apply the three aforementioned generators and FC and PointNet-Mix discriminators to our dataset, but find jet structure is not adequately reproduced. GraphCNN’s local convolutions make learning global structure difficult, and while the TreeGAN and FC generator + PointNet discriminator combinations are improvements, they are not able to learn multi-particle correlations, particularly for the complex top quark jets, nor deal with the variable-sized light quark jets to the extent necessary for physics applications. We thus aim to overcome limitations of existing GANs by designing novel generator and discriminator networks that can learn such correlations and handle variable-sized particle clouds.

Acknowledgements

This chapter is, in part, a reprint of the materials as they appear in R. Kansal. “Symmetry Group Equivariant Neural Networks,” (2020); and NeurIPS, 2021, R. Kansal; J. Duarte; H. Su; B. Orzari; T. Tomei; M. Pierini; M. Touranakou; J.-R. Vlimant; and D. Gunopulos. Particle Cloud Generation with Message Passing Generative Adversarial Networks. The dissertation author was the primary investigator and author of these papers.