3.3 Gauge theories
Nature seems to take advantage of the simple mathematical representations of the symmetry laws. When one pauses to consider the elegance and the beautiful perfection of the mathematical reasoning involved and contrast it with the complex and far-reaching physical consequences, a deep sense of respect for the power of the symmetry laws never fails to develop. — C. N. Yang
So far, we have discussed spin- scalar bosons (and the spin- fermions in Appendix B.4); the last set of SM particles are the spin- gauge bosons. These are the particles which mediate all three fundamental forces in the SM: electromagnetism, the weak force, and the strong force. Fortunately, compared to spinors, they live in the simpler and familiar vector representation of the Lorentz group.
On the other hand, they are intrinsically tied to a unique type of internal, local, symmetry in QFT: gauge symmetry. Unlike, say, Lorentz or spacetime translation invariance, this is not a fundamental physical symmetry of nature, and is not associated with any consrervation law. Instead, it simply describes a redundancy in our mathematical formulation of the gauge theory, stemming from the fact that the vector fields used to describe the gauge bosons have more degrees of freedom (DoFs) than the physical particles themselves. The DoFs are thereby reduced by identifying fields related by a gauge symmetry transformation to be the same physical state, known as the principle of gauge invariance. This is entirely analogous to requiring that a change of coordinate system not affect the physics. A deeper discussion of the motivations behind gauge invariance can be found in Appendix B.5.1.
In this section, we first introduce the simplest gauge boson, the photon, and its associated gauge symmetry in Section 3.3.1. Coupling this to matter and quantizing the theory gives us QED, the relativistic quantum theory of electromagnetism (Section 3.3.2). We then generalize this to, and quantize, non-abelian gauge theories, known as Yang-Mills theories, in Sections 3.3.3 and 3.3.3., respectively. We conclude with a discussion of renormalization and the running of coupling constants in Section 3.3.4.
3.3.1 Maxwell Theory
Gauge symmetries are a generalization of internal global symmetries, such as the symmetry from Section 3.1.2, to a local symmetry, where the symmetry transformation can be a function of spacetime. We are most familiar with this concept from classical E&M, in which Maxwell’s laws are invariant under transformations of the -vector potential of the form:
|
| (3.3.1) |
for an arbitrary function , where is a conventional constant that we will soon interpret as the coupling constant of the theory.
Recall that is related to the electric and magnetic fields, and , by:
|
| (3.3.2) |
and the Maxwell equations can be derived from the Lagrangian:
|
| (3.3.3) |
where
|
| (3.3.4) |
is the field strength tensor. One can confirm that (1) and, hence, the Lagrangian is invariant under the gauge transformation in Eq. 3.3.1, and (2) the resulting E-L EOMs are exactly the homogeneous Maxwell equations. Thus, classical E&M was our earliest and simplest gauge theory, although the significance and generalization of gauge invariance only became clear with the advent of QFT.
Gauge invariance significantly restricts the possible terms in the Lagrangian (and thus considerably simplifies the theory). Notably, mass terms like violate gauge invariance, which is why gauge bosons are necessarily massless, without something special like the Higgs mechanism (Section 3.4). As discussed in Appendix B.5.1, gauge invariance also ensures the renormalizability of the theory and reduces the DoFs of such that, once quantized, we can identify it as the photonic field.
Interactions with scalars
The nature of the gauge transformation becomes more apparent when we try to couple the photon to other particles. Note that our Lagrangian above contains terms of the form so (and indeed all spin- fields) have dimension .
Let us consider a scalar field : we can write renormalizable, scalar terms like and ; however, they do not look gauge invariant. To make them so, we must require that also transforms under the same gauge transformation in a way that compensates the change in .
The simplest way is to take to be a complex scalar field and “promote” its inherent global symmetry to a local one:
|
| (3.3.5) |
where we say represents the charge of under the symmetry.10 We can then define the covariant derivative acting on as:11
|
| (3.3.6) |
where is the same coupling constant from Eq. 3.3.1.
One can check that transforms under the gauge transformation as:
|
| (3.3.7) |
meaning provides us with a gauge invariant interaction term for the Lagrangian. Thus, we have a gauge invariant scalar QED Lagrangian:
|
| (3.3.8) |
Note that the commutator of the covariant derivative is in fact not a derivative at all, but proportional to the field strength tensor:
|
| (3.3.9) |
Thus, we can define , which will prove useful for non-abelian gauge symmetries later in this section.
Generally, we choose the normalization for the electron field, so becomes our familiar elementary charge (in natural units) and is the famous dimensionless fine structure constant.12
Interactions with spinors
The case for spinors is not so different. The definition of the covariant derivative remains the same, so combining the “covariant” Dirac Lagrangian with the free photonic yields the QED Lagrangian:
|
| (3.3.10) |
This is in fact the most general possible Lorentz-invariant, renormalizable, -symmetric Lagrangian for a spinor field with a gauge symmetry, and can thus be derived from the requirement of gauge invariance alone (as done in e.g. Peskin and Shroeder [81] Chapter 15.1). This is a general feature of the SM: every possible term permitted by gauge invariance and the usual physical requirements of Lorentz invariance etc. is included in the Lagrangian (with one possible exception that forms the basis for the strong CP problem [102, 103]).
Expanding out the Lagrangian, we have:
|
| (3.3.11) |
where we see this interaction term is simply with the conserved current associated with the global symmetry we found in Section B.4.3. One can check that the E-L EOMs for now correspond to the inhomogeneous Maxwell equations with a source term :
|
| (3.3.12) |
reproducing our beloved E&M from this field theory formulation!
3.3.2 Quantum electrodynamics
The quantized version of the above is what we call quantum electrodynamics (QED): the QFT of electromagnetic interactions. It has proven an extraordinarily successful theory, serving as a model for the remainder of the SM as well as theories for condensed matter phenomena.
The exact path to quantizing depends on the choice of gauge. We will forego those details and simply use physical intuition — namely, that the photon has only two physical, transverse polarizations — to motivate the result:
|
| (3.3.13) |
where are the two transverse polarization basis vectors and and are the photon annihilation and creation operators.
The photon propagator depends as well on the choice of gauge. Expanding the homogeneous photon EOM, Eq. 3.3.12, gives:
|
| (3.3.14) |
which in momentum space becomes:
|
| (3.3.15) |
Recall that the propagator is the inverse of the operator on the LHS for a delta-function source; however, due to the redundant DoFs of , this is not directly invertible without first fixing a gauge.
The cleanest way to do so is to add a “Lagrange multiplier” term representing the gauge fixing condition to the Lagrangian. The most common choice is the Lorenz gauge, , which makes Lorentz-invariance manifest and to enforce which we can include the term . One can confirm that the EOM for is exactly the Lorenz gauge condition. Inverting the new EOM for gives us the (Feynman) photon propagator:
|
| (3.3.16) |
This is called the gauge and different values of correspond to different propagators, each with their own advantages and disadvantages for calculations. In QED, we typically take , called the Feynman-’t Hooft gauge, for simplicity:
|
| (3.3.17) |
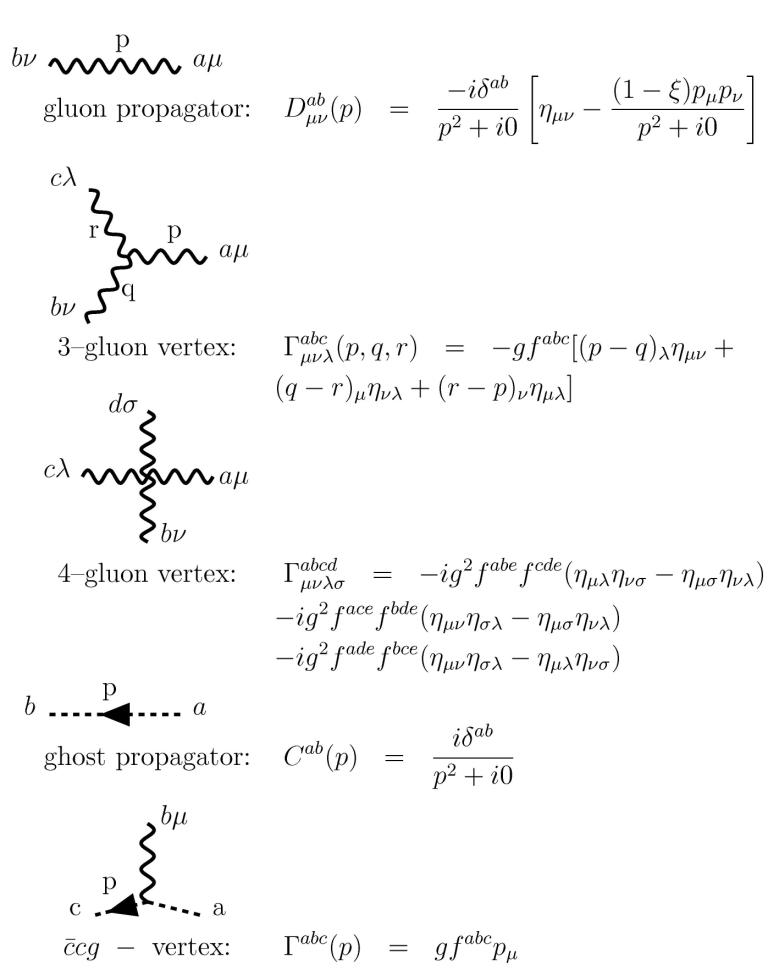
Definition 3.3.1. With this, we can write down the Feynman rules for QED, with spinor (, ) and -vector (, ) indices labeled explicitly for clarity:
These Feynman rules can be applied to simple tree-level processes similarly to Yukawa theory (see Sections 3.2.3 and B.4.5). These include several important processes such as electron-electron scattering via a virtual photon, Compton scattering , electron-positron annihilation , and electron-positron (or Bhabha) scattering . The former (and its variations with other charged particles) is what we generally experience as electromagnetism, and can recover the Coloumb potential in the non-relativistic limit.
3.3.3 Yang-Mills Theory
Following the remarkable success of QED and GR, a generalization of such gauge theories to non-abelian symmetries was proposed by Chen Ning Yang and Robert Mills in 1953 [104], today referred to as Yang-Mills theories. These theories picked up steam in the 1960s when the concept of spontaneous symmetry breaking was developed to give mass to the gauge bosons (Section 3.4) and it was realized that both the weak and strong interactions can be described by and Yang-Mills theories, respectively. They are hence a cornerstone of the SM, and we will now briefly outline their construction, generalizing the gauge symmetry from the previous section.
Non-abelian gauge transformations
In Yang-Mills theory, we allow non-gauge fields to transform locally under any Lie group , in an arbitrary representation of the group (generally, in the SM, is either the fundamental or trivial representation). This means the fields are actually vectors of (on top of their usual spinor or -vector indices etc.), and transform as:
|
| (3.3.18) |
where are the generators of in the representation and is the gauge transformation. To construct a -invariant Lagrangian, we again need to define a covariant derivative with gauge fields connecting the local transformations of across spacetime:
|
| (3.3.19) |
Observe that we must have as many gauge fields as there are group generators to counter all possible gauge transformations ; i.e., there are s, living in the adjoint representation of (see Chapter 2.2). The gauge field is often represented more conveniently as a “Lie-algebra-valued” field (i.e., as an object in the Lie algebra):
|
| (3.3.20) |
We can derive how transforms by requiring the covariant derivative to transform identically to (the same as in the abelian case):13
|
| (3.3.21) |
where is the coupling constant. One can check this is satisfied for the transformed gauge field:
|
| (3.3.22) |
For infinitesimal gauge transformations , this can be written in terms of the components as:
|
| (3.3.23) |
where are the structure constants of the Lie algebra of . The second term represents the gauge transformation, same as in the abelian case, while the third term is new and is the transformation property for a field in the adjoint representation.
The field strength tensor
The final piece we need for the Lagrangian is a gauge-invariant kinetic term for the gauge fields, generalizing the electromagnetic field strength tensor . We can construct this, as in the abelian case, using the commutator of covariant derivatives:
|
| (3.3.24) |
Again, this reduces to the E&M tensor for an abelian symmetry, where the commutator term is . In the non-abelian case, the commutator term adds new self-interaction terms to the gauge fields. One can check that transforms as:
|
| (3.3.25) |
or, infinitesimally, in terms of components as:
|
| (3.3.26) |
which we can recognize as the transformation of a field in the adjoint representation (Eq. 3.3.23 without the gauge transformation term).
Clearly, for non-abelian theories, the field-strength tensor alone, or even , is no longer gauge-invariant; however, its trace is:
|
| (3.3.27) |
using the cyclic property of the trace, providing us with a gauge-invariant kinetic term for the gauge fields. In terms of components, this is:
|
| (3.3.28) |
The value of is a normalization constant that is conventionally chosen to be for the fundamental representation. Expanding out gives us cubic and quartic self-interaction terms for the gauge fields.
The Yang-Mills Lagrangian
Combining all of the above, we have the gauge-invariant Yang-Mills Lagrangian:
|
| (3.3.29) |
or, in explicit, component form:
|
| (3.3.30) |
where the indices and are running over the fermion fields in the representation . Note again that a mass term would violate gauge invariance without the Higgs mechanism.
Interestingly, despite the extra self-interaction terms, there remains only one free parameter in the theory: the coupling constant . This is why the SM, despite its apparent complexity, has so few free parameters, particularly in the “gauge sector” (the majority of free parameters are related to couplings in the Higgs sector). It is also worth emphasizing that the primary difference physically between abelian and non-abelian gauge theories is that the gauge bosons are charged under the gauge group in the latter (and, hence, self-interact).
Quantum Yang-Mills Theory
The form of the quantized gauge fields in Yang-Mills are similar to the case, except now with the extra adjoint representation indices. The process of quantization and deriving the propagator, however, is considerably more involved for non-abelian theories. The core idea of adding an gauge-fixing term to the Lagrangian is similar, but due to the gauge fields’ non-trivial transformation property, the proper treatment necessitates the introduction of imaginary internal particles called Faddeev-Popov ghosts to cancel gauge-dependent terms. Somewhat similar to virtual particles, these ghosts are purely mathematical artifacts required to maintain gauge- and Lorentz-invariance of the quantized theory. The full details of this process can be found in e.g. Peskin and Shroeder [81] Chapter 16; the upshot is simply some extra Feynman rules involving ghost particles in the theory.
The new Feynman rules for non-abelian Yang-Mills theories are shown in Figure 3.5. The gauge bosons are conventionally referred to as “gluons” but these rules are general. Note the cubic and quartic gauge boson vertices, as well as the ghost particle () diagrams, unique to non-abelian theories. The phenomenology of Yang-Mills theories in the SM will be discussed in the next chapter.
3.3.4 Running couplings and asymptotic freedom
As discussed briefly in Section 3.2, in order to handle divergences from higher order “loop” diagrams in perturbation theory, a class of mathematical techniques called renormalization is employed. A perhaps surprising physical consequence of this is that parameters of the theory are dependent on the energy scale at which they are probed. Their dependence is described the renormalization group equations or flow.
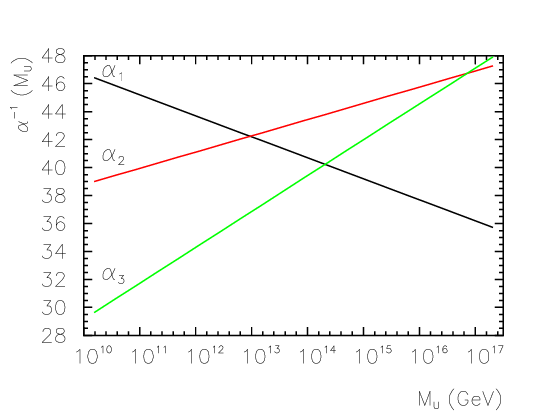
The renormalization group is an extremely deep subject with applications in many areas of physics. The most relevant result for us is the running of the coupling constants in gauge theories — i.e., the strength of the corresponding forces as a function of the energy scale. This is shown for the relevant , , and gauge symmetries of the SM in Figure 3.6.
We see firstly that the electromagnetic interaction strength increases with energy scale. Physically, this is understood through the vacuum polarization via virtual electron-positron pair creation, which “screen” the electric charges of real particles more effectively at longer distances, thereby weakening the force.14
A notable, Nobel-prize winning, 1973 result of Frank Wilczek, David Gross, and David Politzer, however, was an inverse dependence on energy for non-abelian gauge theories [105, 106], as shown for the and couplings in Figure 3.6.15 This phenomenon is called asymptotic freedom, as in the high energy limit the theory is effectively one of free particles. It is a notable feature of the strong force, as will be discussed in Chapter 4.1.
10Note that such a transformation is not possible with a real field, which necessarily has charge and does not couple with the photon.
11As discussed above, this is the same concept as the covariant derivative in GR, with the gauge field acting as a connection on a fiber bundle analogously to the Levi-Civita connection between tangent bundles. Essentially, it encodes the change in the local phase of across spacetime (see Peskin and Shroeder [81] Chapter 15.1 for a nice derivation of this).
12Technically, this value varies with our energy scale, as we will discuss in Section 3.3.4, and is its asymptotic value at low energies.
13For a detailed derivation see e.g. Ricardo Matheus’ QFT Lectures [83] Part 34.
14Interestingly, QED has a Landau pole: a finite value of the energy scale for which the interaction strength is infinite. However, this value is so high () as to have no practical consequence, and likely points to the breakdown of perturbation theory, that is used to derive the running coupling, at such a scale.
15Technically, this depends on the gauge group and the number of fermions in the theory; for both the weak and strong forces, this number is sufficiently small (see e.g. Peskin and Shroeder [81] Chapter 16).