4.3 The Higgs sector

The Higgs boson, being the only scalar in the SM and uncharged under the $U{(1)}_{\mathrm{EM}}$ and $\mathrm{SU}{(3)}_C$ symmetries, may appear to be the simplest particle in the theory. However, these same properties also mean that the Higgs sector is not as strongly constrained by gauge invariance, renormalizability, etc. as the gauge and fermionic sectors. Indeed, the Higgs sector contains the majority of the free parameters of the SM: the Yukawa couplings (12 masses of the fermions $+$ 8 more parameters from the CKM and PMNS matrices), the Higgs VEV, and the Higgs mass (or, equivalently, $\lambda$ in the Higgs potential). Without it, the SM would only have three free parameters: the three forces’ coupling constants!

This is why a significant motivation for the next decades of the LHC, as well as future “Higgs factory” colliders, is to precisely characterize the Higgs sector. In this section, we first describe how this is possible at the LHC and discuss recent experimental constraints. We then motivate measurements of Higgs pair production, both in the SM and through BSM decays of heavy resonances, which are the focus of this dissertation and a key target of the current and upcoming LHC physics program.

4.3.1 Higgs boson production and measurements at the LHC

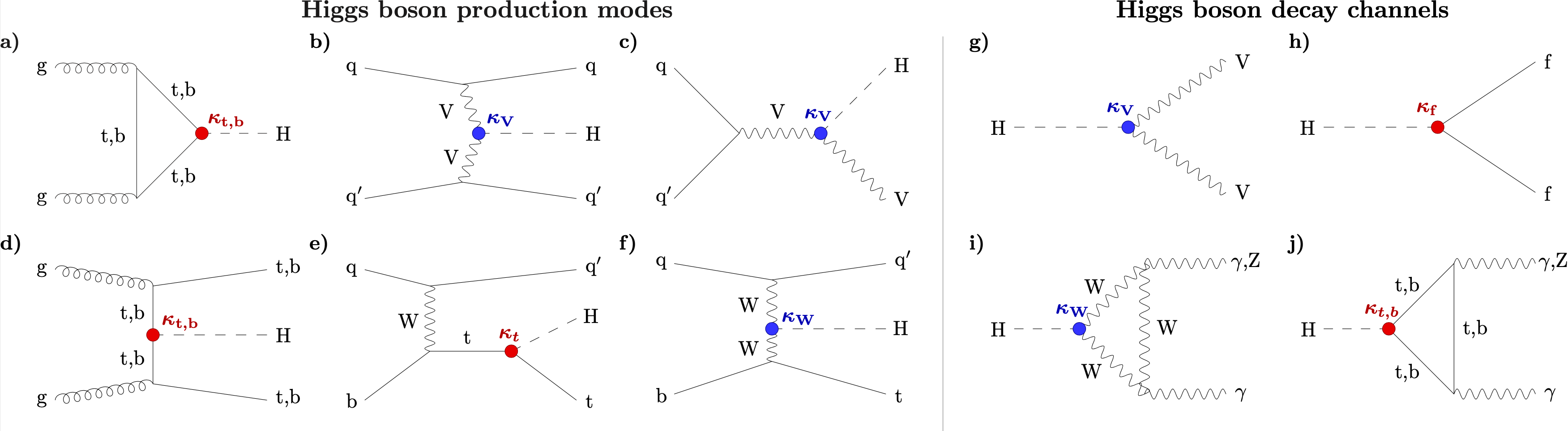
Higgs bosons are produced at the LHC through a variety of parton-parton interactions, as shown in Figure 4.17. Because of their high mass, they have a lifetime of roughly $O(10^{-22})$s and decay immediately into two vector bosons or two fermions at tree-level, with further decays possible through loops. The decay probability depends on the strength of the respective interactions, which we see from Section 4.2 are proportional to the mass or the mass squared for fermions and vector bosons, respectively, though with the probability lowered for decays that are not kinematically accessible (i.e., when the total mass of the decay products is greater than the Higgs’).

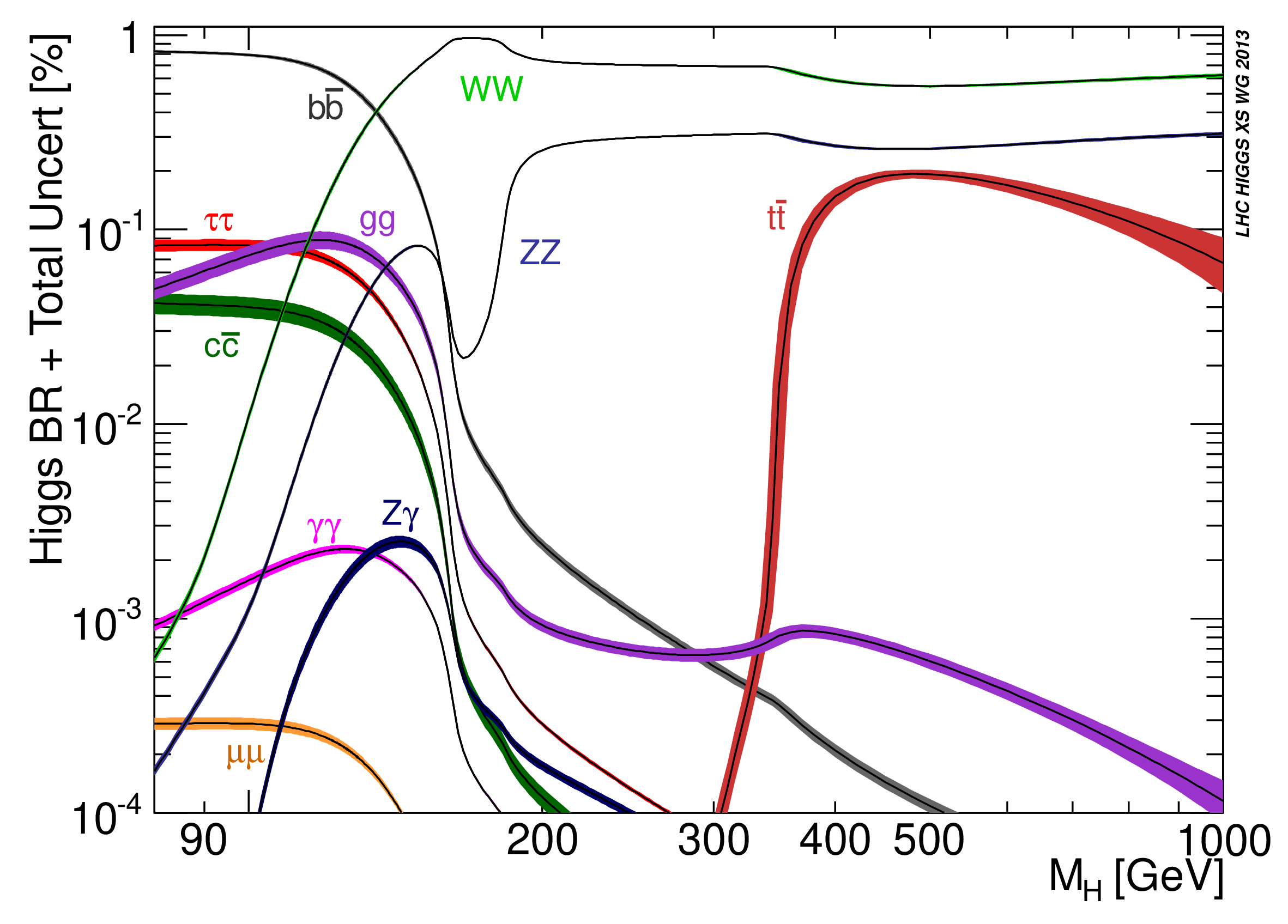
This is illustrated in Figure 4.18, which shows the branching fractions (BFs) of the Higgs boson as a function of its mass. Generally, we see the higher the mass of the decay product, the higher the BF; however, as the Higgs mass decreases, first the $t\overline{t}$ and later the $W$ and $Z$ boson decays become kinematically inaccessible, leading to decreasing decay probabilities.

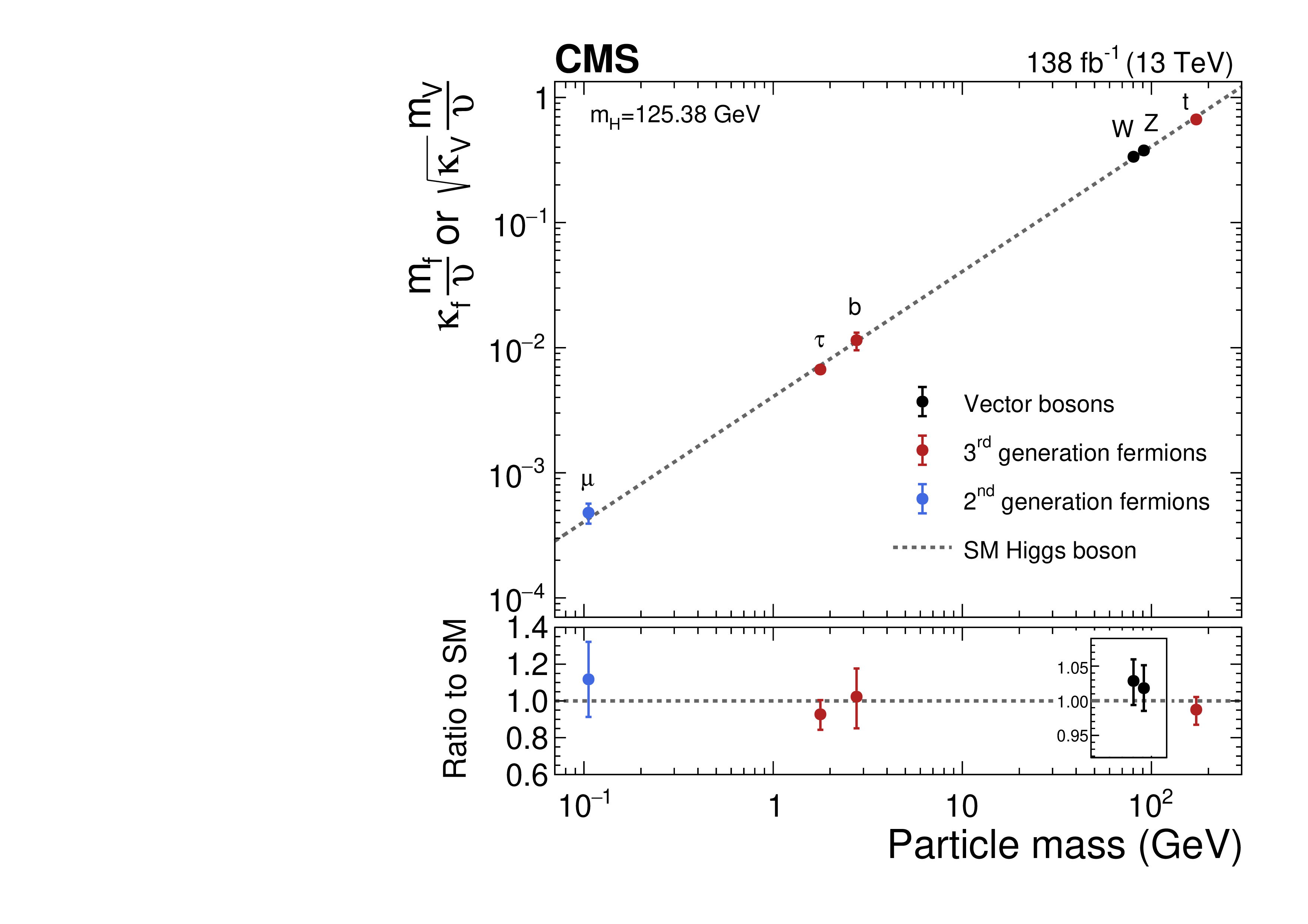
The Higgs boson was initially observed by the CMS and ATLAS experiments in 2012 through a combination of several decay channels. Since then, the two experiments have been making steady progress in the precise measurements of the various Higgs properties. For example, Figure 4.19 shows the overall constraints on the Higgs to fermion and vector boson couplings and the Higgs mass by the CMS experiment. Constraints are based on the $\kappa$-framework [157], where ${\kappa }_X$ scales the Higgs-$X$ coupling strength with ${\kappa }_X=1$ corresponding to the SM prediction. Changes to the coupling strength due to new physics are thus generically captured by deviations from ${\kappa }_X=1$.

4.3.2 Higgs pair production in the SM

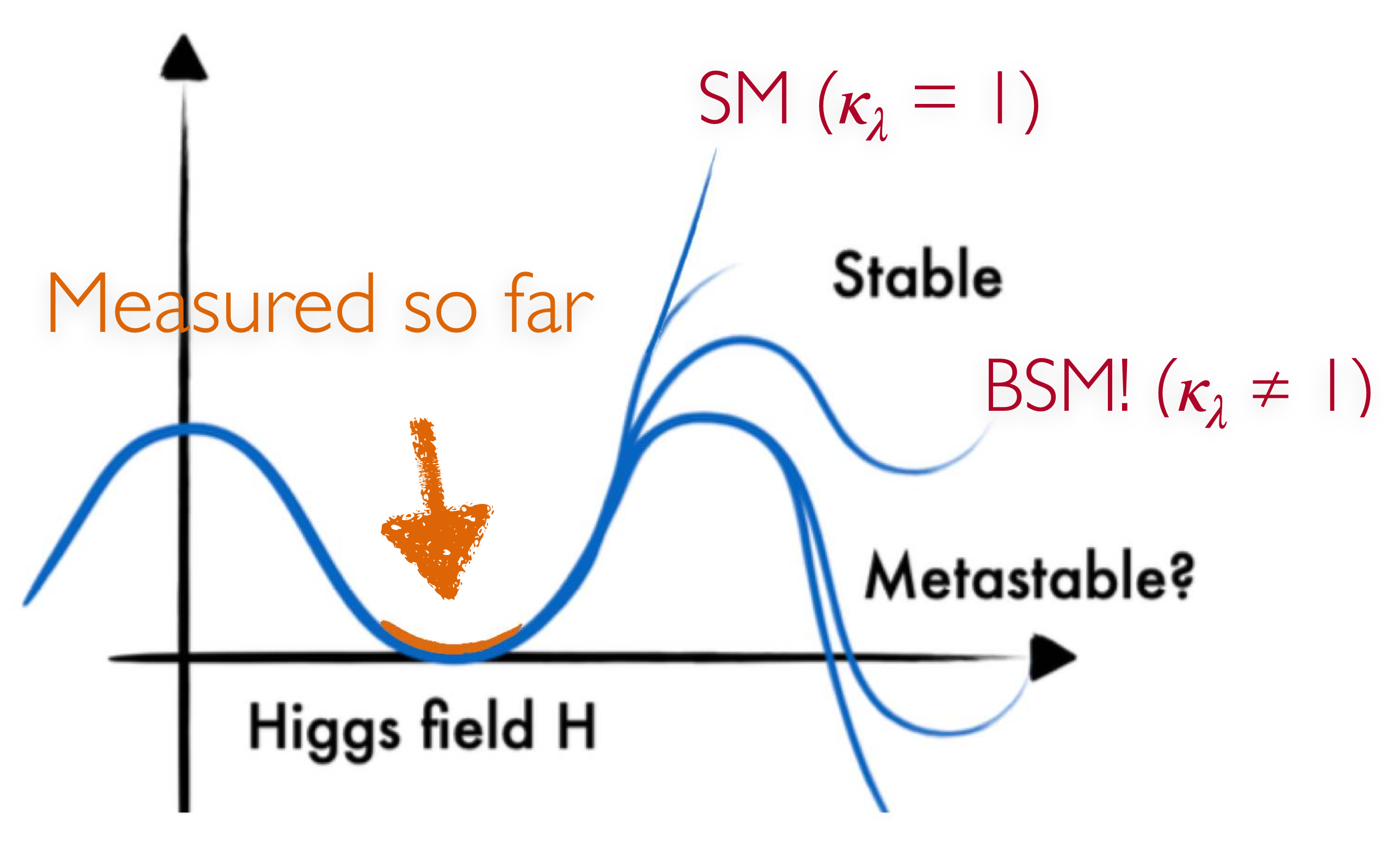
Two couplings of the Higgs boson which have not been well-constrained are the trilinear Higgs self-coupling ($\mathrm{\text{H}}\mathrm{\text{H}}\mathrm{\text{H}}$), with coupling modifier ${\kappa }_{\lambda }$, and the Higgs quartic coupling to vector bosons ($\mathrm{\text{H}}\mathrm{\text{H}}\mathrm{\text{V}}\mathrm{\text{V}}$), with modifier ${\kappa }_{2\mathrm{\text{V}}}$. As discussed in Section 4.2.3 and illustrated in Figure 4.20, measuring the Higgs self-coupling in particular is necessary to fully characterize the Higgs potential, deviations to which could hint at BSM explanations to mysteries such as baryon asymmetry [158]. As we describe below, both couplings can be probed exclusively through Higgs pair production ($\mathrm{\text{H}}\mathrm{\text{H}}$), which is why it is a key physics target for the upcoming high-luminosity era of the LHC.

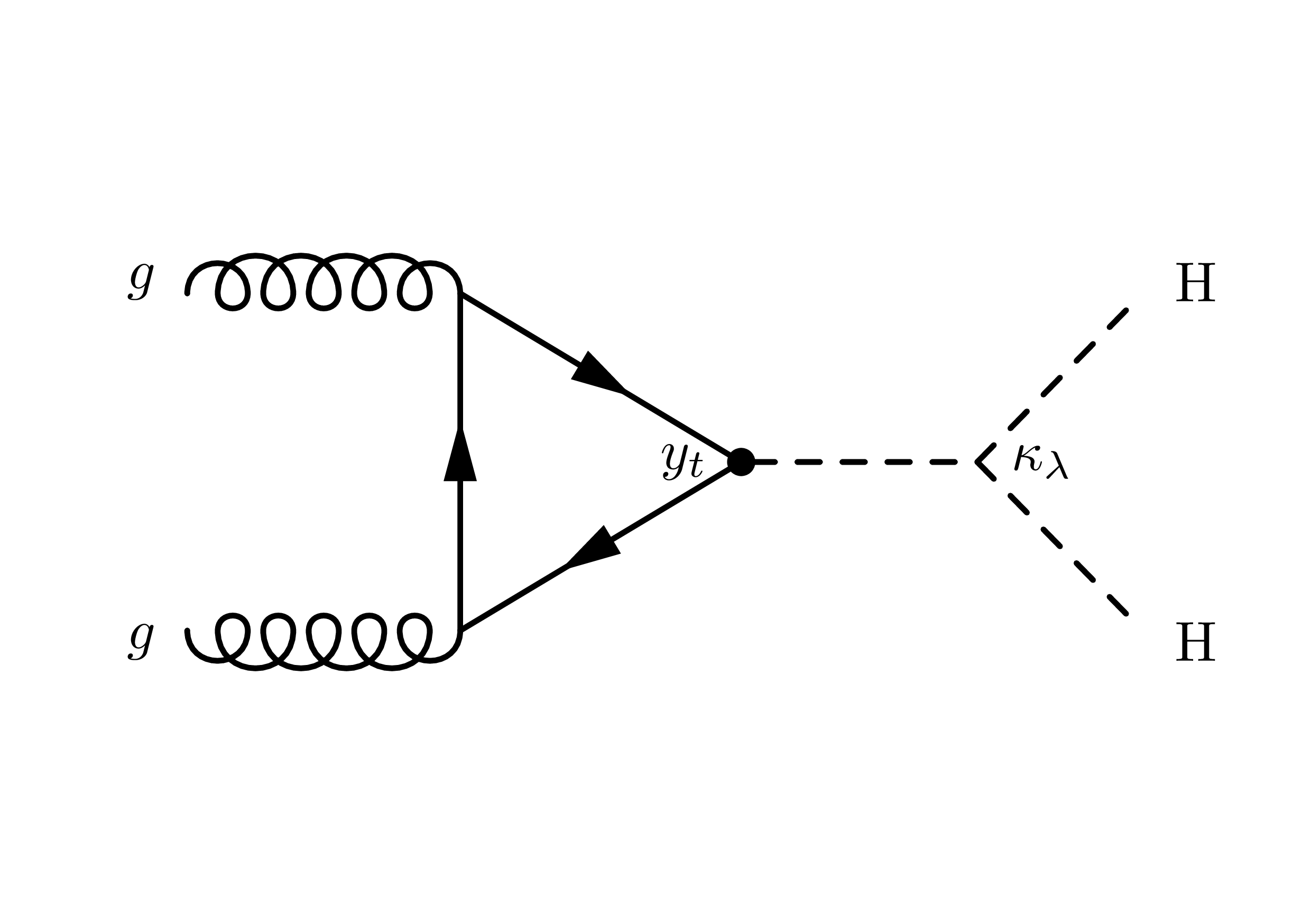
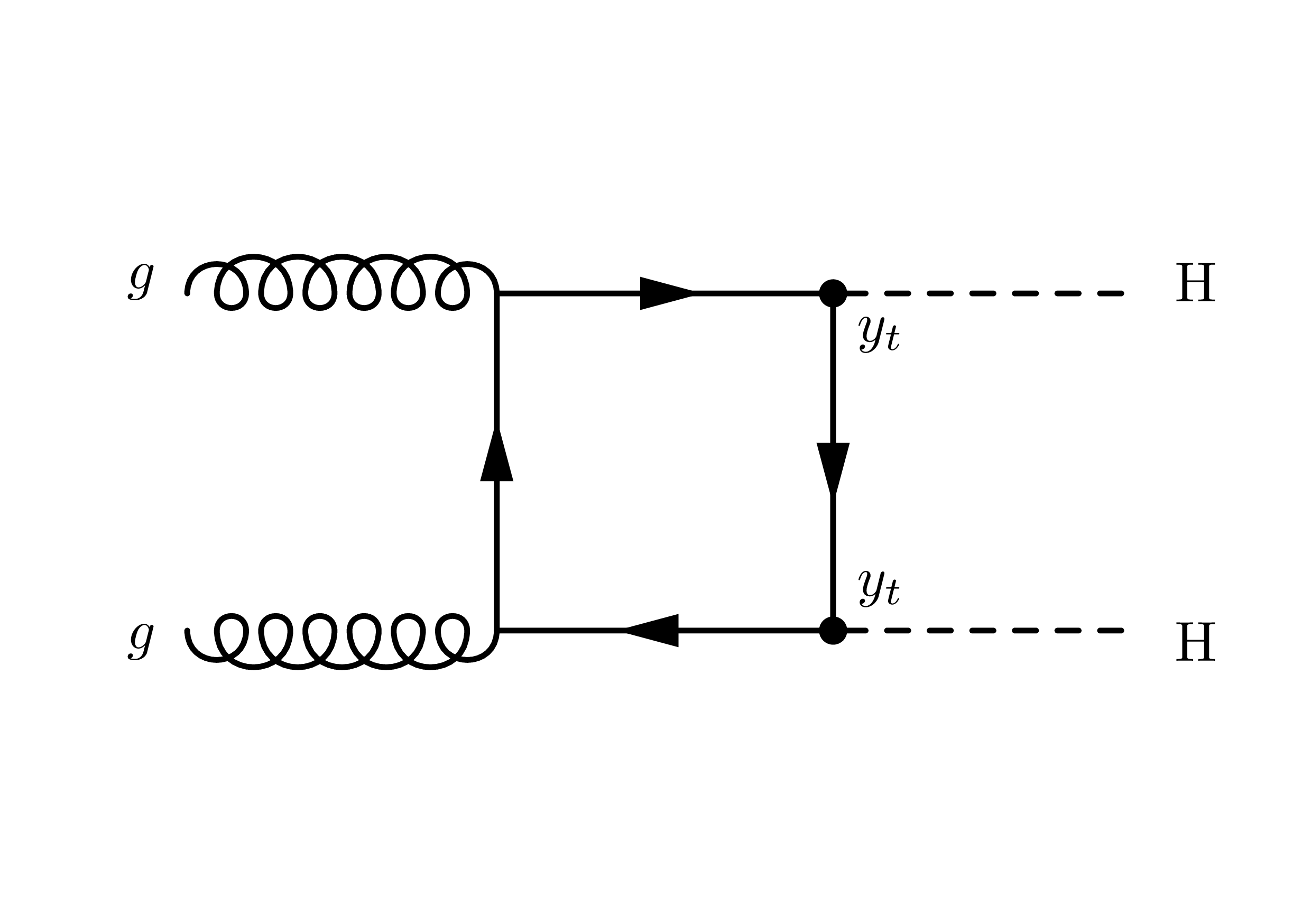
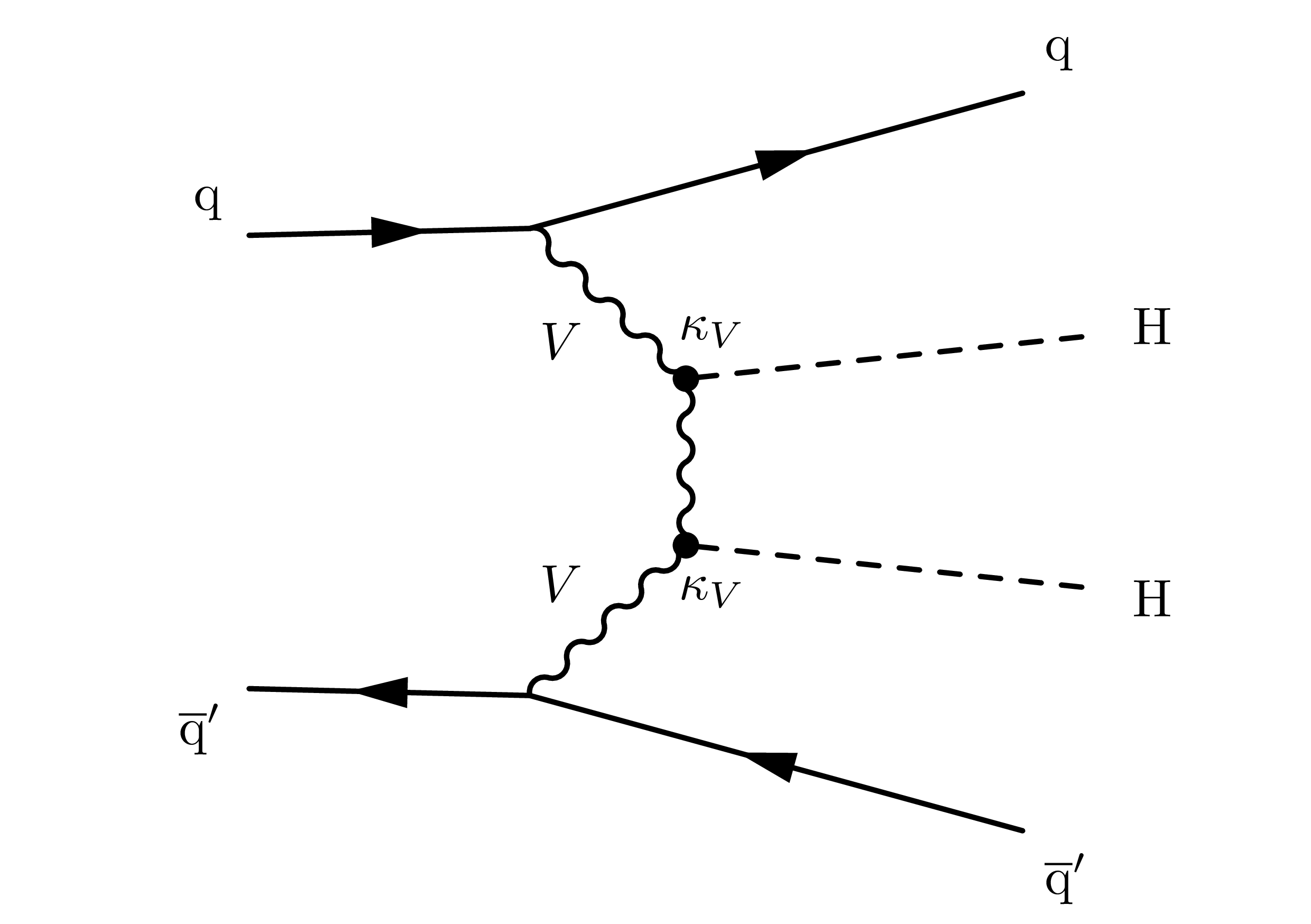
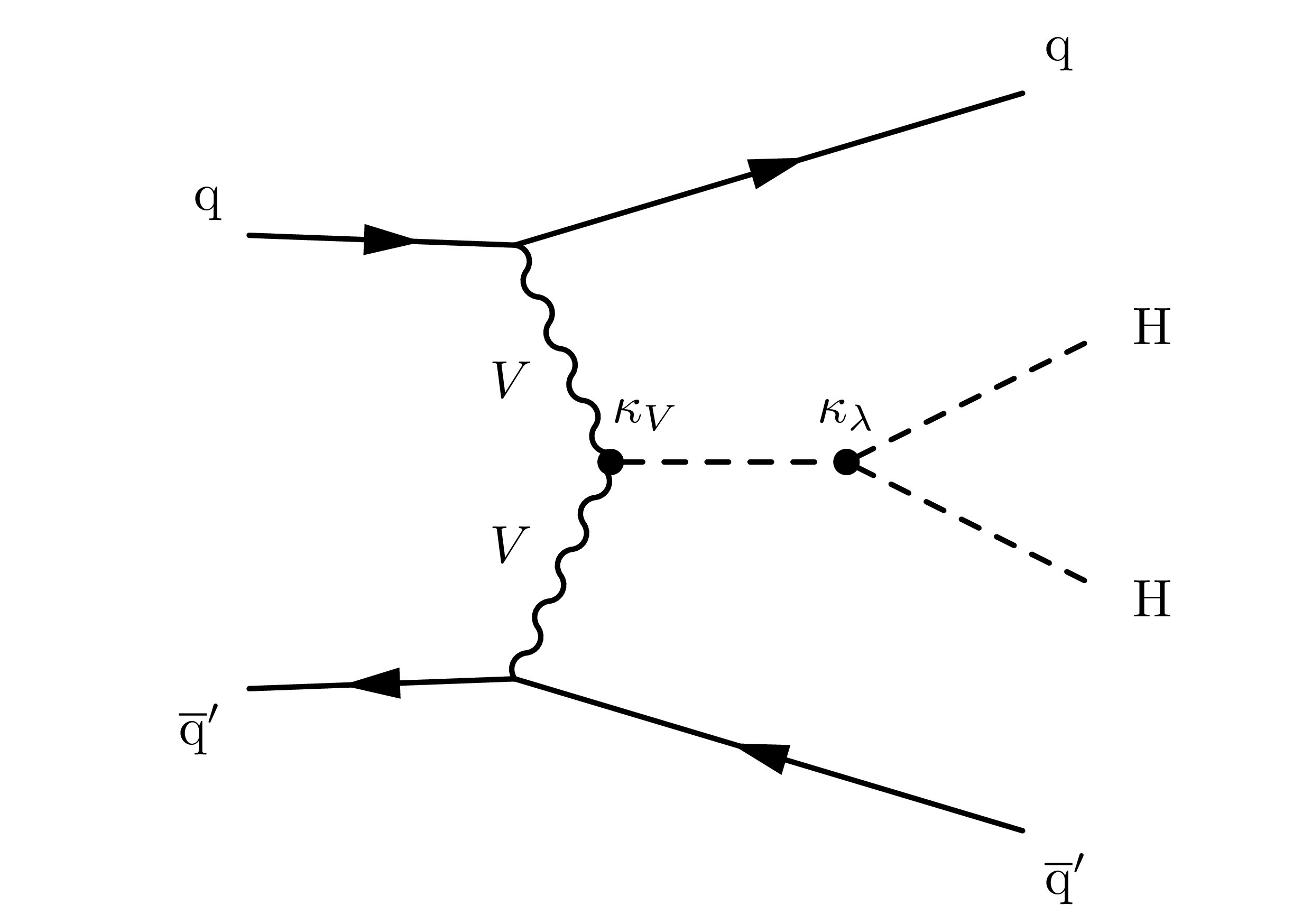
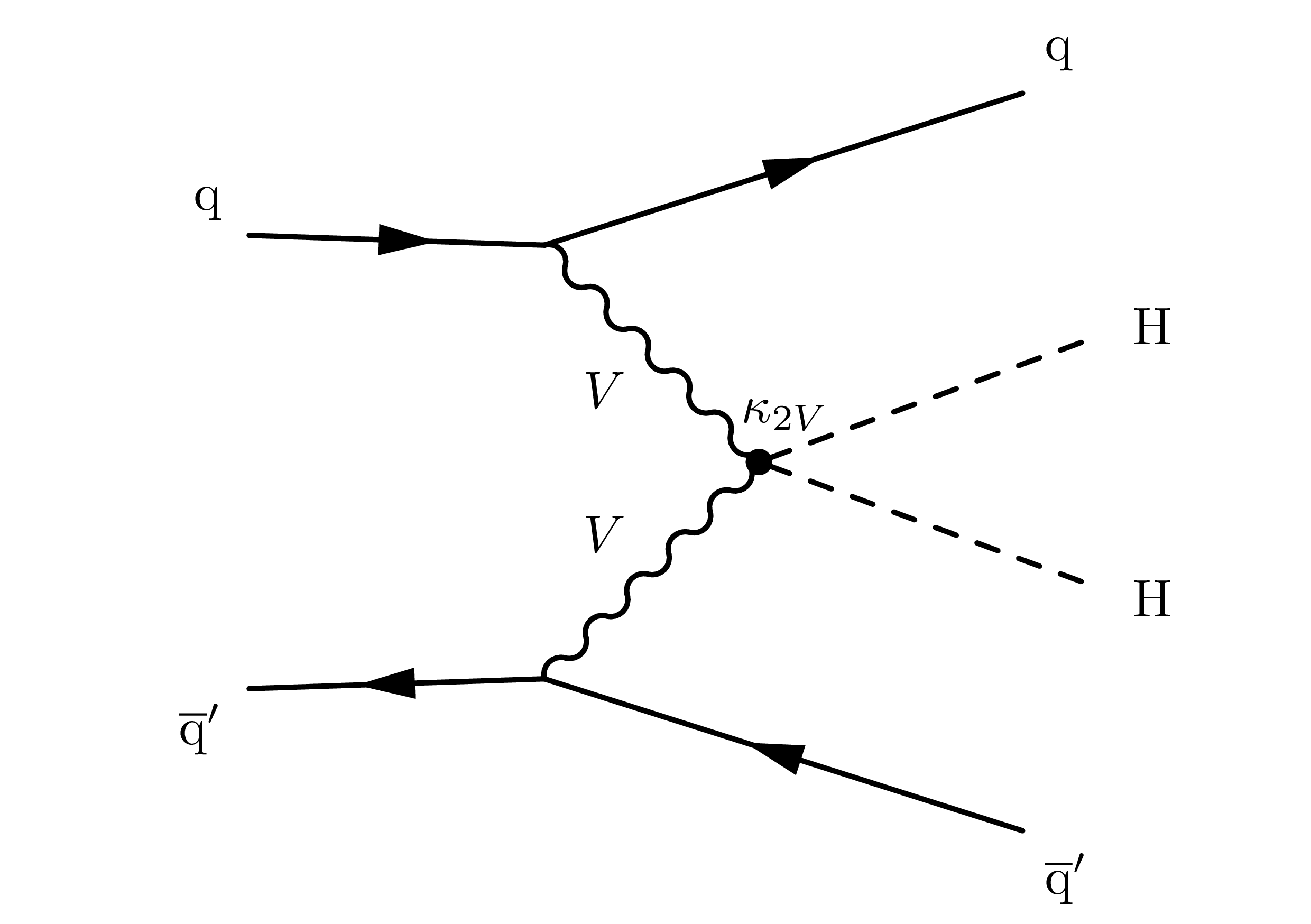
$\mathrm{\text{H}}\mathrm{\text{H}}$ production in the SM occurs dominantly through gluon fusion (ggF), with a small production cross section ${\sigma }_{\mathrm{ggF}}=31.05_{-5.0\%}^{+2.2\%}\pm 3\%{(\mathrm{\text{PDF}}+{\alpha }_s)}_{-18\%}^{+4\%}(m_{\mathrm{\text{t}}})\text{ fb}$ [159, 160] at a center of mass energy of 13$\text{TeV}$ and $m_{\mathrm{\text{H}}}=125\text{GeV}$, and subdominantly through vector boson fusion (VBF), with a smaller production cross section ${\sigma }_{\mathrm{VBF}}=1.726_{-0.04\%}^{+0.03\%}\pm 2.1\%(\mathrm{\text{PDF}}+{\alpha }_s)\text{ fb}$ [25]. At leading order, the ggF production mode has contributions from diagrams that involve the trilinear $\mathrm{\text{H}}\mathrm{\text{H}}\mathrm{\text{H}}$ Higgs self-coupling and the emission of two Higgs bosons through a top quark loop, while the VBF production mode has contributions from three diagrams involving the trilinear $\mathrm{\text{H}}\mathrm{\text{H}}\mathrm{\text{H}}$, $\mathrm{\text{H}}\mathrm{\text{V}}\mathrm{\text{V}}$, and quartic $\mathrm{\text{H}}\mathrm{\text{H}}\mathrm{\text{V}}\mathrm{\text{V}}$ couplings (Figures 4.21 and 4.22). It also features the distinct final state signature of two, typically forward, jets in addition to the two Higgs bosons.

The production cross section and kinematic properties of the $\mathrm{\text{H}}\mathrm{\text{H}}$ system are altered if values of the Higgs self-coupling, the top Yukawa coupling, and/or the quartic $\mathrm{\text{H}}\mathrm{\text{H}}\mathrm{\text{V}}\mathrm{\text{V}}$ coupling are modified due to beyond the SM (BSM) effects. Notably, at the energy scale of the LHC, the leading contribution to the VBF production amplitude is the scattering of longitudinal vector bosons, which scales as $\sim m_{\mathrm{\text{H}}\mathrm{\text{H}}}^2({\kappa }_{2\mathrm{\text{V}}}-{\kappa }_{\mathrm{\text{V}}}^2)$ [161], where, as above, ${\kappa }_{\lambda }$, ${\kappa }_{2\mathrm{\text{V}}}$, and ${\kappa }_{\mathrm{\text{V}}}$ are defined to be multiplicative modifiers of the $\mathrm{\text{H}}\mathrm{\text{H}}\mathrm{\text{H}}$, $\mathrm{\text{H}}\mathrm{\text{H}}\mathrm{\text{V}}\mathrm{\text{V}}$, and $\mathrm{\text{H}}\mathrm{\text{V}}\mathrm{\text{V}}$ couplings from their SM values, respectively.

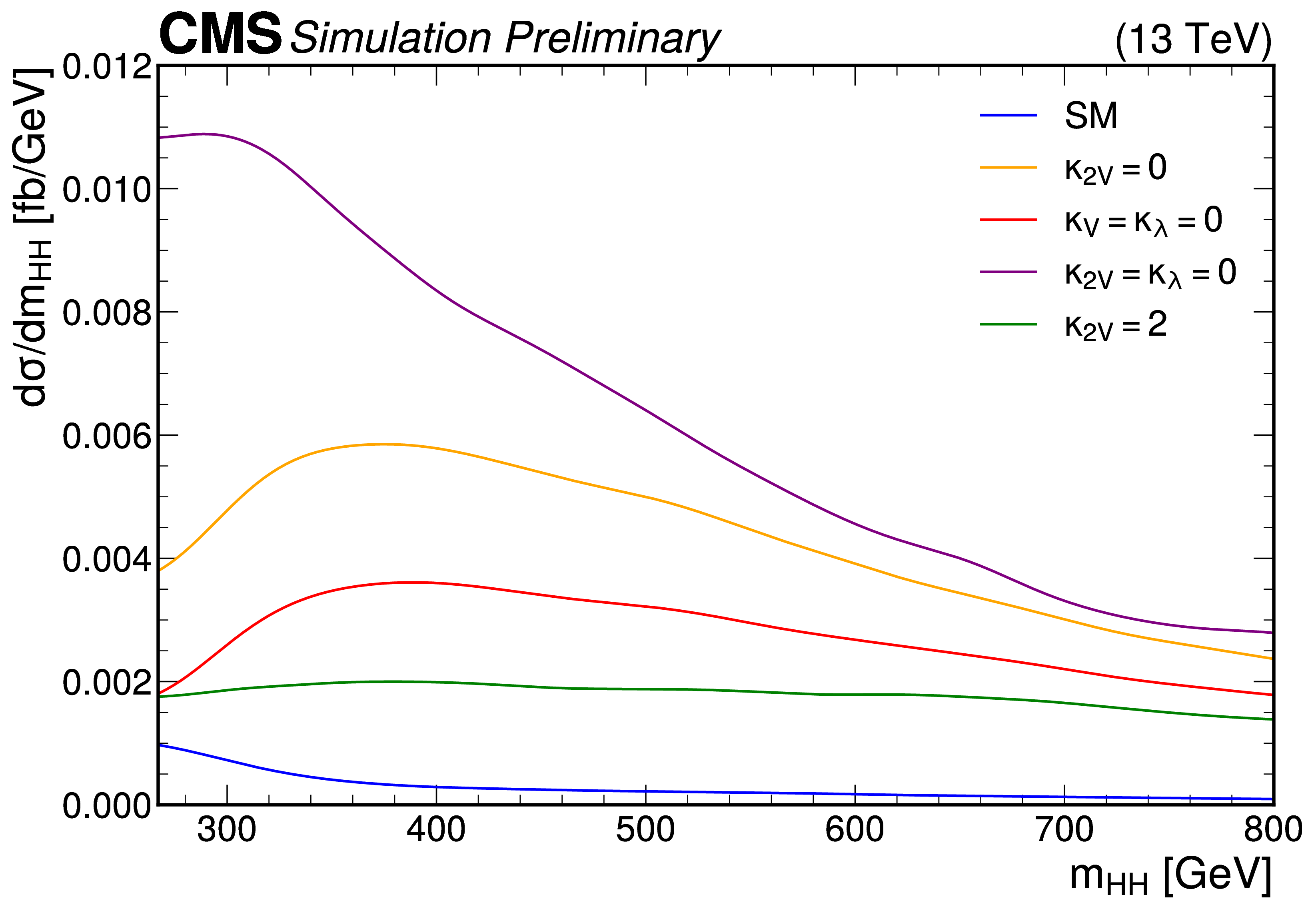
In the SM, with ${\kappa }_{2\mathrm{\text{V}}}={\kappa }_{\mathrm{\text{V}}}=1$, VBF production is suppressed since the left-most ${(\mathrm{\text{H}}\mathrm{\text{V}}\mathrm{\text{V}})}^2$ and right-most $\mathrm{\text{H}}\mathrm{\text{H}}\mathrm{\text{V}}\mathrm{\text{V}}$ VBF diagrams in Figure 4.22 cancel; however, BSM deviations to $\mathrm{\text{H}}\mathrm{\text{H}}\mathrm{\text{V}}\mathrm{\text{V}}$ can spoil the cancelation, significantly enhancing this mode. This departure from the SM could be more visible at high energies, as illustrated in Figure 4.23, which shows the increase and shift towards higher $m_{\mathrm{\text{H}}\mathrm{\text{H}}}$ of the differential VBF $\mathrm{\text{H}}\mathrm{\text{H}}$ production cross section for enhanced and reduced ${\kappa }_{2\mathrm{\text{V}}}$ values. Thus, measuring high-$m_{\mathrm{\text{H}}\mathrm{\text{H}}}$ nonresonant VBF $\mathrm{\text{H}}\mathrm{\text{H}}$ production, with both Higgs bosons highly Lorentz-boosted, is a powerful probe of the $\mathrm{\text{H}}\mathrm{\text{H}}\mathrm{\text{V}}\mathrm{\text{V}}$ coupling.

This is evidenced by the current ${\kappa }_{2\mathrm{\text{V}}}$ constraint in CMS being dominated by the search for boosted $\mathrm{\text{H}}\mathrm{\text{H}}$ in the $\mathrm{\text{b}}\overline{\mathrm{\text{b}}}\mathrm{\text{b}}\overline{\mathrm{\text{b}}}$ channel, with an observed (expected) 95% confidence level (CL) constraint of $[0.6,1.4]$ ($[0.7,1.4]$), excluding ${\kappa }_{2\mathrm{\text{V}}}=0$ for the first time [162]. This is followed by CMS searches in the resolved $\mathrm{\text{b}}\overline{\mathrm{\text{b}}}\mathrm{\text{b}}\overline{\mathrm{\text{b}}}$ [28] and $\mathrm{\text{b}}\overline{\mathrm{\text{b}}}\mathit{\tau \tau }$ [29] channels, with constraints of $[-0.1,2.2]$ ($[-0.4,2.5]$) and $[-0.4,2.6]$ ($[-0.6,2.8]$), respectively. Similarly, the strongest ${\kappa }_{2\mathrm{\text{V}}}$ constraint from the ATLAS experiment is from the boosted $\mathrm{\text{b}}\overline{\mathrm{\text{b}}}\mathrm{\text{b}}\overline{\mathrm{\text{b}}}$ search [163], with an observed (expected) 95% CL constraint of $[0.55,1.49]$ ($[0.3,1.7]$).

The success of searches in the boosted $\mathrm{\text{b}}\overline{\mathrm{\text{b}}}\mathrm{\text{b}}\overline{\mathrm{\text{b}}}$ channel motivates further exploration of high-$m_{\mathrm{\text{H}}\mathrm{\text{H}}}$ $\mathrm{\text{H}}\mathrm{\text{H}}$ production. This dissertation presents the first search in the all-hadronic $\mathrm{\text{b}}\overline{\mathrm{\text{b}}}\mathrm{\text{V}}\mathrm{\text{V}}$ channel, where one Higgs boson decays to $\mathrm{\text{b}}\overline{\mathrm{\text{b}}}$ while the other to $\mathrm{\text{W}}\mathrm{\text{W}}$ or $\mathrm{\text{Z}}\mathrm{\text{Z}}$, where $\mathrm{\text{W}}\to \mathrm{\text{q}}\overline{\mathrm{\text{q}}}$ and $\mathrm{\text{Z}}\to \mathrm{\text{q}}\overline{\mathrm{\text{q}}}$. The branching fractions for the $\mathrm{\text{b}}\overline{\mathrm{\text{b}}}$ and all-hadronic $\mathrm{\text{V}}\mathrm{\text{V}}$ decays are $0.58$ and $0.11$ respectively, for a total branching fraction $B(\mathrm{\text{H}}\mathrm{\text{H}}\to \mathrm{\text{b}}\overline{\mathrm{\text{b}}}(\mathrm{\text{V}}\mathrm{\text{V}}\to 4\mathrm{\text{q}}))=2\cdot 0.58\cdot 0.11=0.13$, which is the second largest behind $\mathrm{\text{b}}\overline{\mathrm{\text{b}}}\mathrm{\text{b}}\overline{\mathrm{\text{b}}}$. The analysis primarily aims to constrain ${\kappa }_{2\mathrm{\text{V}}}$ and also sets an exclusion limit on the inclusive $\mathrm{\text{H}}\mathrm{\text{H}}$ production cross-section. It is not expected to be sensitive to ${\kappa }_{\lambda }$ because of the focus on the high-$m_{\mathrm{\text{H}}\mathrm{\text{H}}}$ regime.

Another benefit of the high-$m_{\mathrm{\text{H}}\mathrm{\text{H}}}$ regime is the significantly reduced QCD multijet background, which otherwise makes such all-hadronic searches extremely challenging. Because of the two Higgs bosons’ high Lorentz-boosts, this regime also features the unique experimental signature of the $\mathrm{\text{b}}\overline{\mathrm{\text{b}}}$ and $\mathrm{\text{V}}\mathrm{\text{V}}\to 4\mathrm{\text{q}}$ decays each being reconstructed as single wide-radius jets. Such merged $\mathrm{\text{H}}\to \mathrm{\text{b}}\overline{\mathrm{\text{b}}}$ jets have been identified to great effect in CMS using deep neural networks (DNNs) [162, 164], but attaining similar signal versus background discrimination for $\mathrm{\text{H}}\to \mathrm{\text{V}}\mathrm{\text{V}}$ jets remains an open challenge. To this end, we introduce a new attention-based DNN, referred to as the global particle transformer (GloParT) to not only enable this search but open new possibilities for searches in boosted-$\mathrm{\text{V}}\mathrm{\text{V}}$ channels as well (Chapter 13).

4.3.3 Experimental status of $\mathrm{\text{H}}\mathrm{\text{H}}$ measurements with CMS

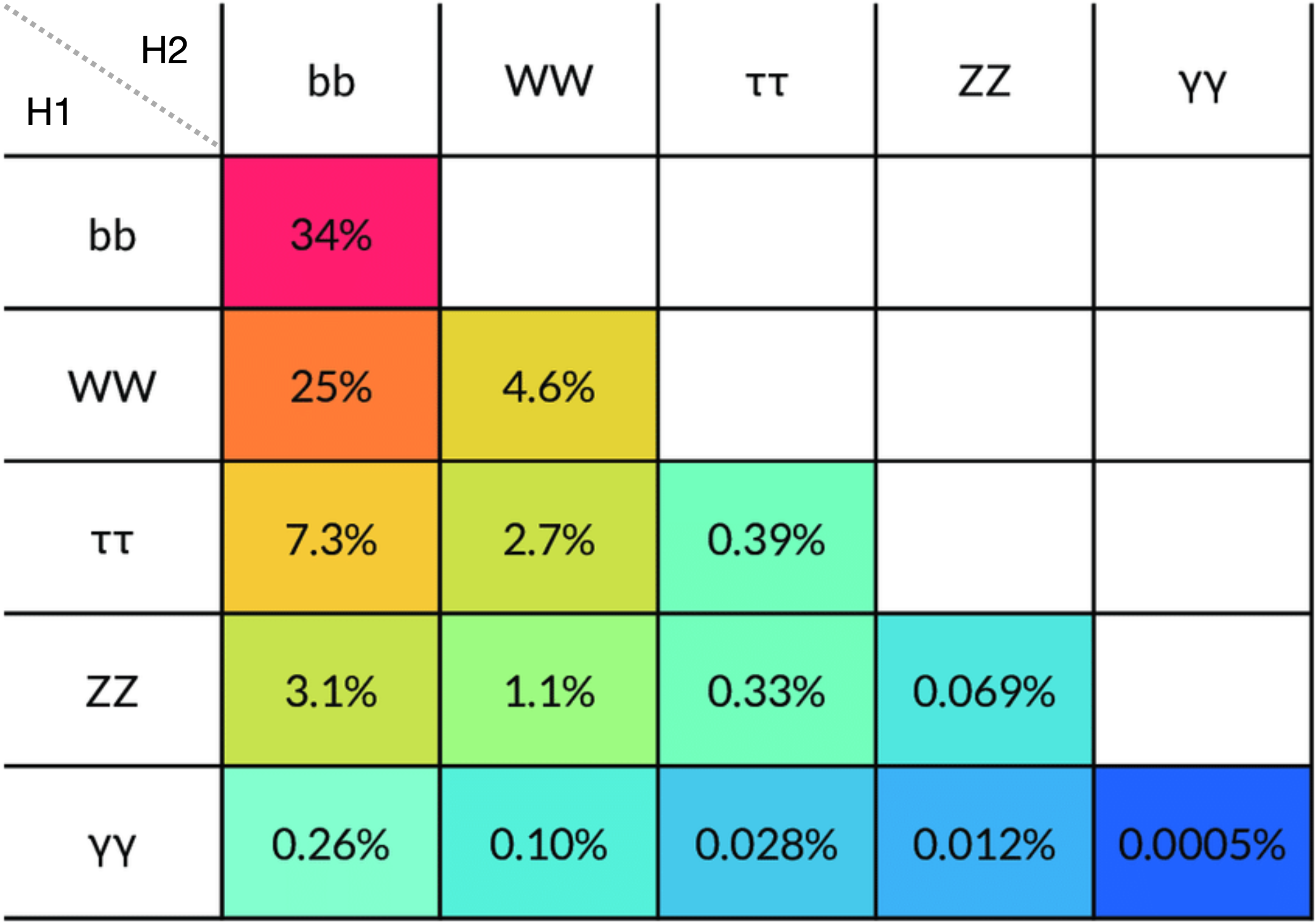
The decays and branching fractions (BFs) of the Higgs boson pairs are shown in Figure 4.24. Three of these final states have emerged as experimental “golden channels” — the channels expected to yield the highest signal-to-background-events ratio for SM $\mathrm{\text{H}}\mathrm{\text{H}}$ production:

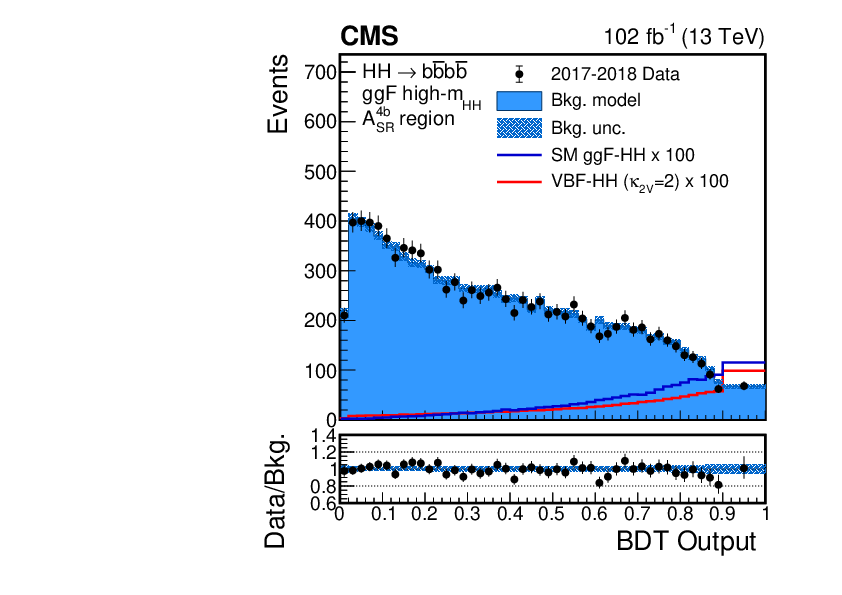
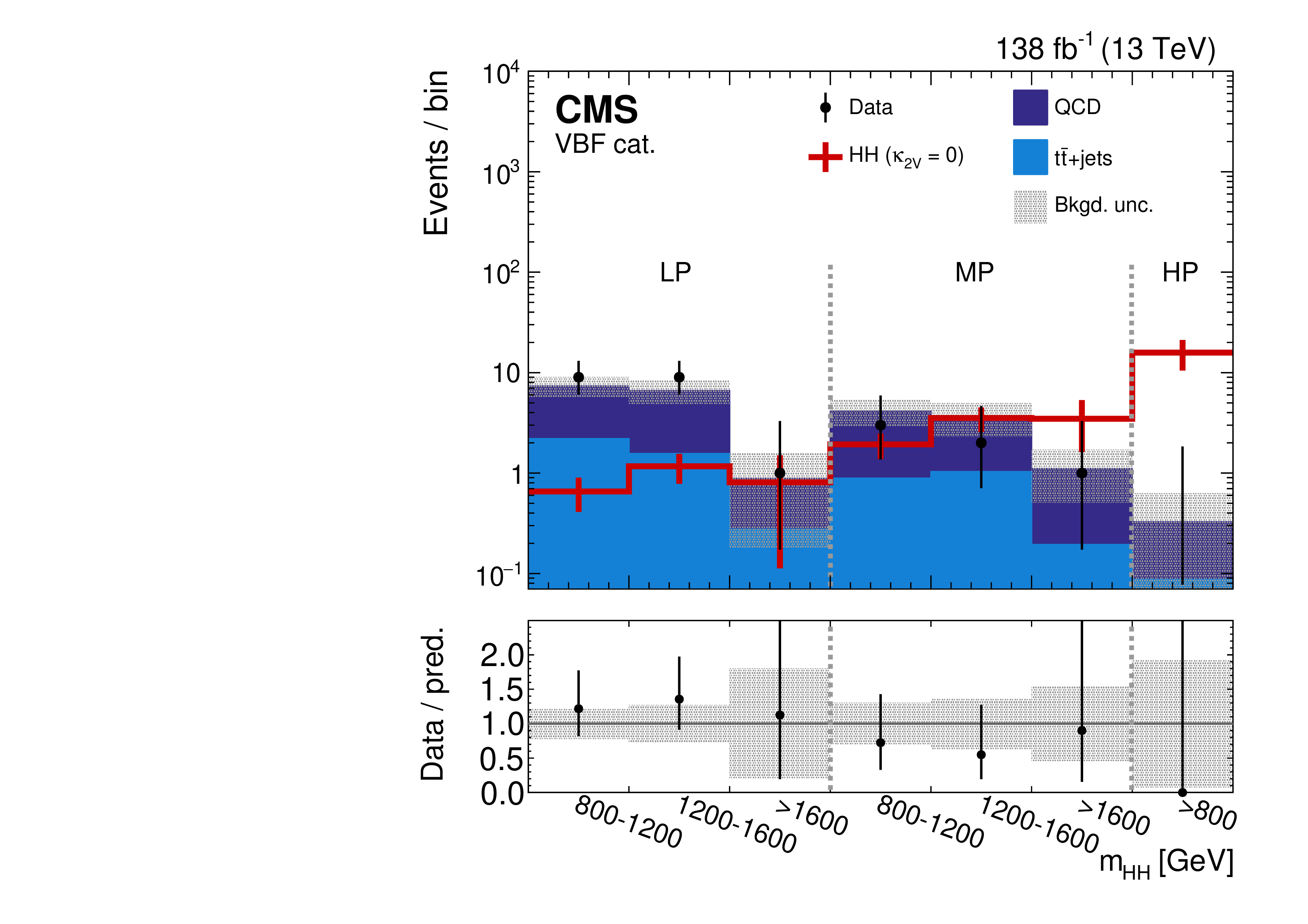
• $\mathrm{\text{b}}\overline{\mathrm{\text{b}}}\mathrm{\text{b}}\overline{\mathrm{\text{b}}}$: This channel has the highest BF ($34\%$) and, despite the large QCD multijet background due to the all-hadronic final state, it benefits from unique signatures of heavy-flavor b-jets, such as the presence of secondary vertices and displaced tracks due to the long lifetimes of b-hadrons. Both the resolved [28] and boosted [162] Run 2 CMS analyses (Figure 4.25) have been highly effective, with the latter benefitting from the high BF of this decay mode, the exponential reduction of the QCD multijet background in the boosted regime, and significant recent advances in $\mathrm{\text{b}}\overline{\mathrm{\text{b}}}$-jet classification and reconstruction (as will be discussed in Chapter 13).
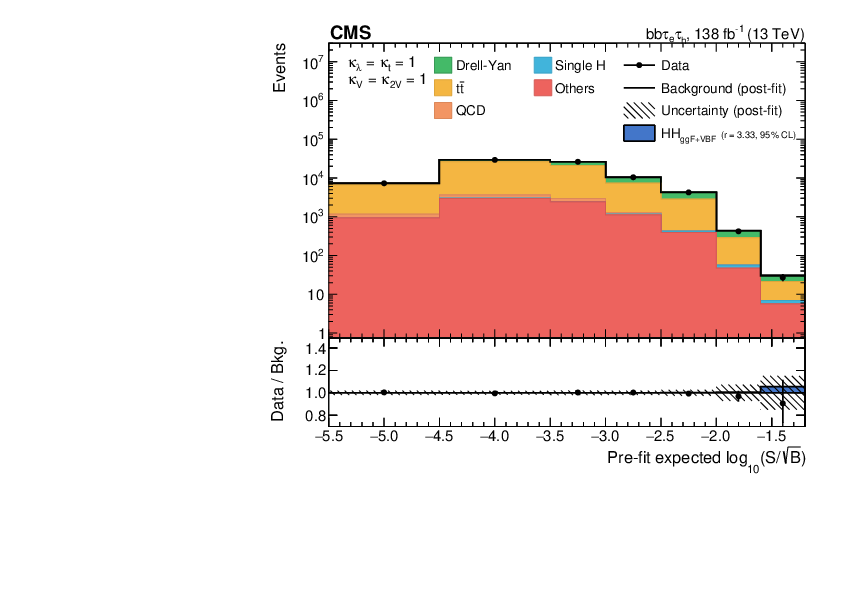
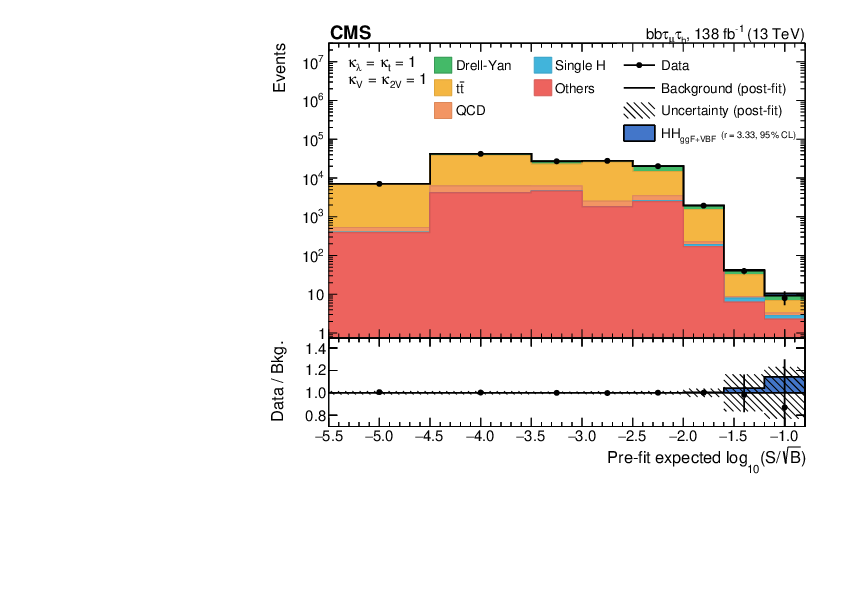
• $\mathrm{\text{b}}\overline{\mathrm{\text{b}}}\mathit{\tau \tau }$: This has an intermediate BF of $7\%$ but relatively lower background of primarily Drell-Yan ($\mathrm{\text{Z}}∕{\gamma }^{\ast }$), top quark pair production ($t\overline{t}$), and QCD multijet events (Figure 4.26, reproduced from Ref. [29]). It benefits from similar deep learning techniques for b-jet tagging, and targets all-hadronic (${\tau }_h{\tau }_h$) and semi-leptonic (${\tau }_h{\tau }_e$ or ${\tau }_h{\tau }_{\mu }$) $\tau$-lepton decays using a variety of traditional and ML techniques.
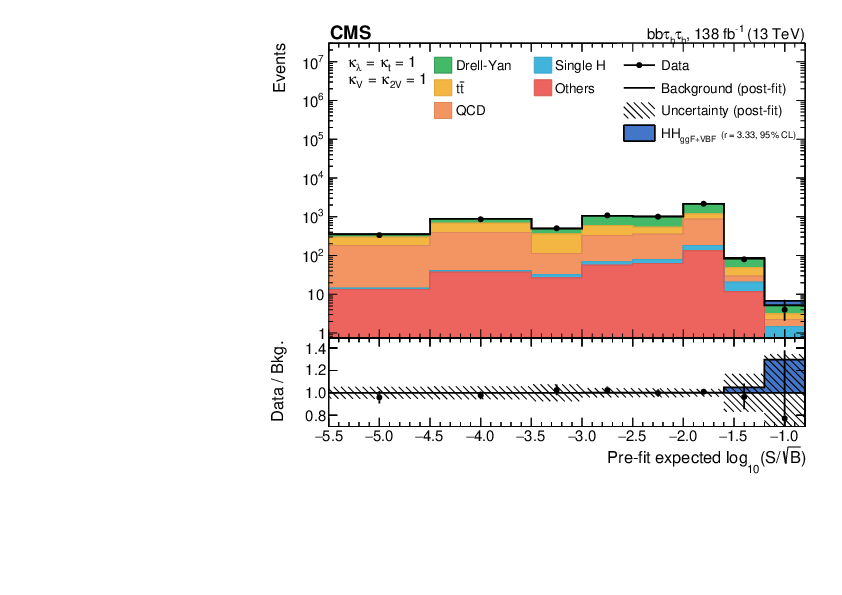
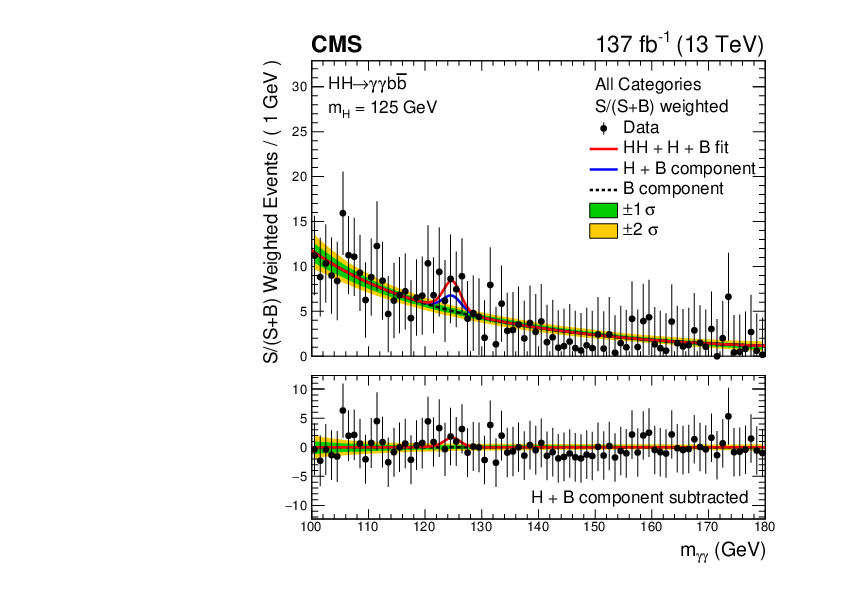
• $\mathrm{\text{b}}\overline{\mathrm{\text{b}}}\mathit{\gamma \gamma }$: Despite the small BF ($0.3\%$) of this channel, the $\mathrm{\text{H}}\to \mathit{\gamma \gamma }$ decay provides a clean experimental signature with a sharply peaking resonance over a small background of QCD multijet + $\gamma$ events (Figure 4.27, from Ref. [30]).

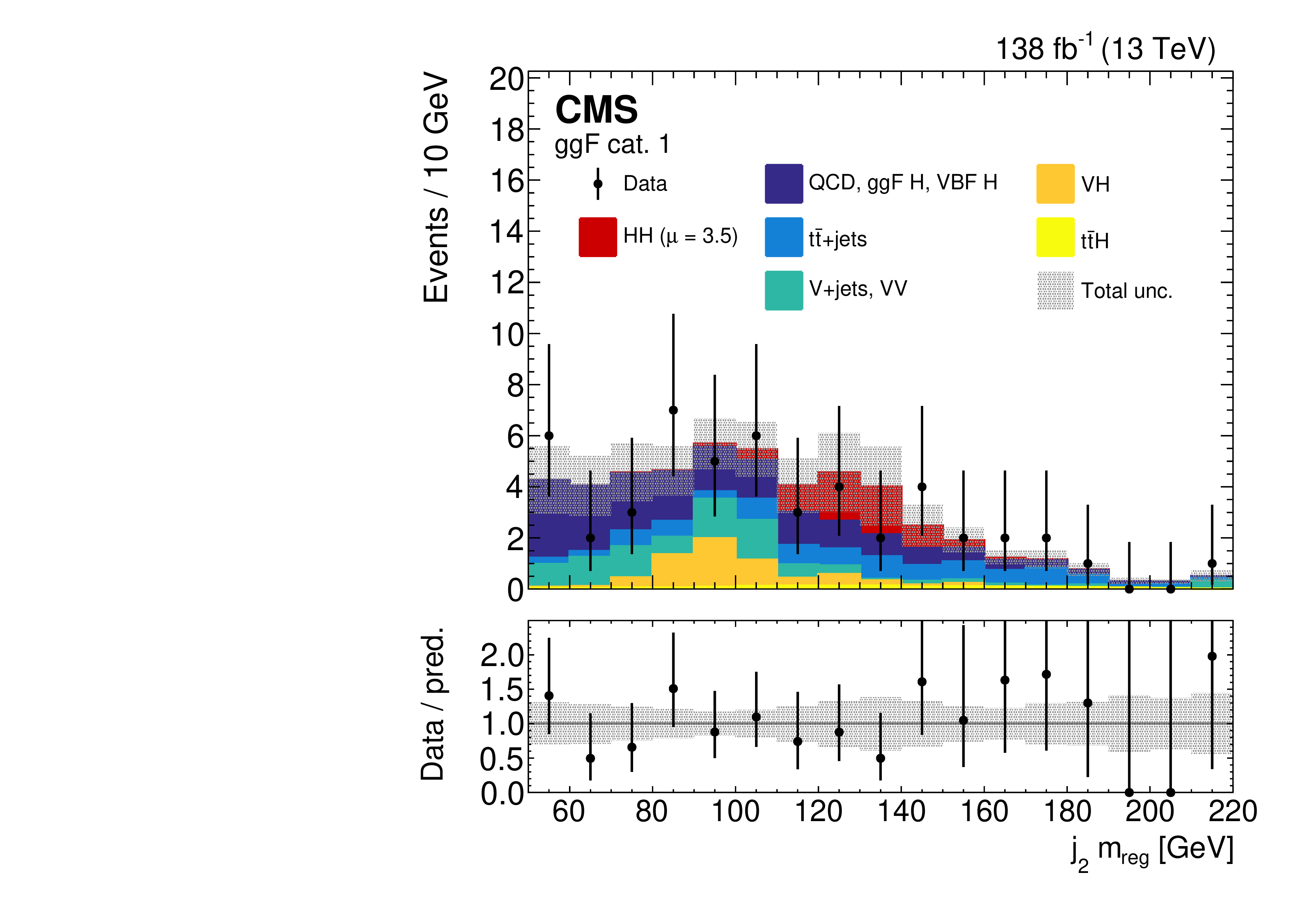
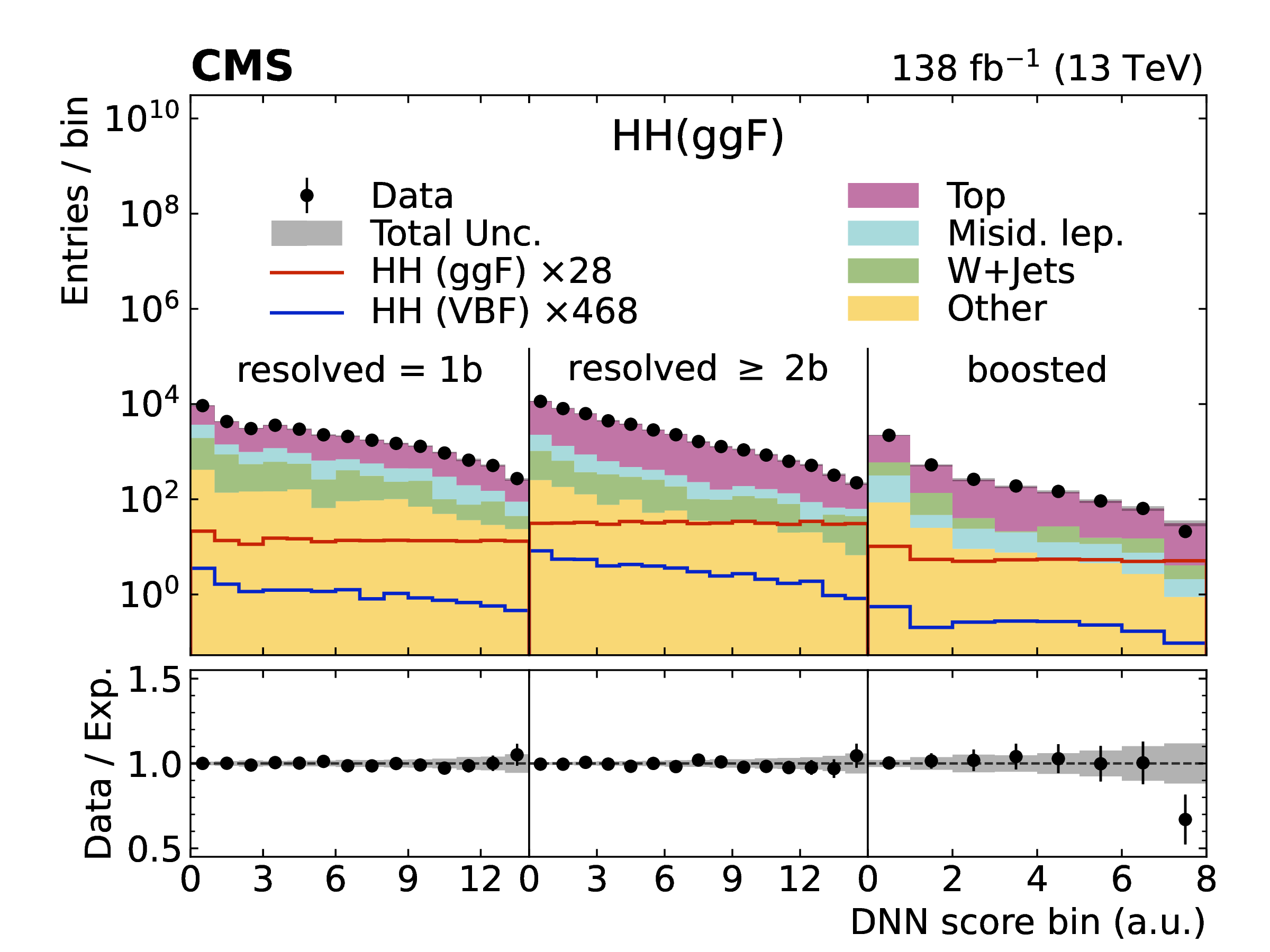
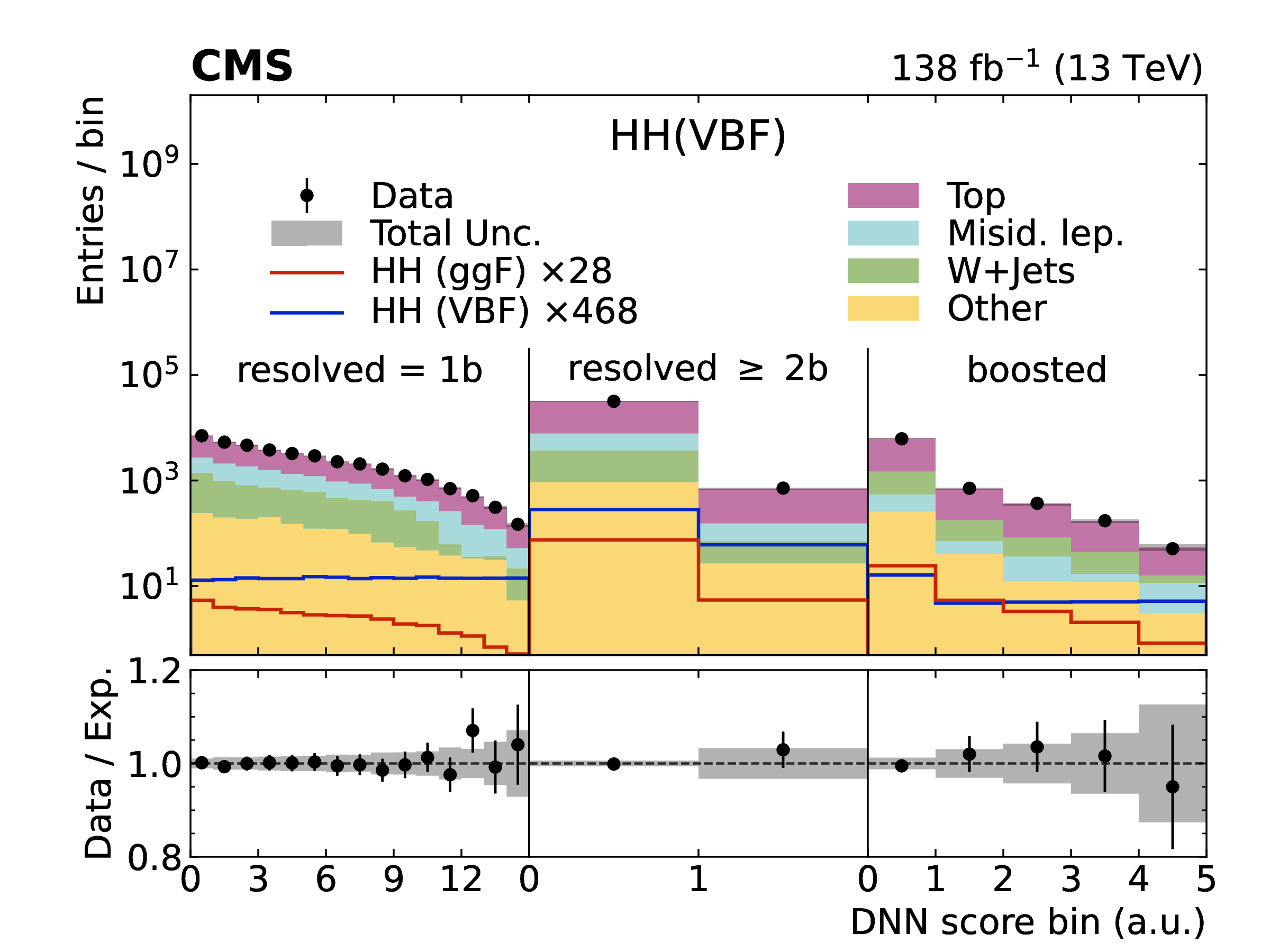
More recently, the $\mathrm{\text{b}}\overline{\mathrm{\text{b}}}\mathrm{\text{W}}\mathrm{\text{W}}$ channel has been explored in the douple-lepton ($\mathrm{\text{l}}\mathrm{\text{l}}\mathit{\nu \nu }$) and single-lepton ($\mathrm{\text{l}}\nu \mathrm{\text{q}}\mathrm{\text{q}}$) $\mathrm{\text{W}}\mathrm{\text{W}}$ final states [31], which have a large combined BF of $13.4\%$. The former features a clean experimental signature of two opposite-sign leptons but a small BF of $2.6\%$, while the latter has the higher BF of 10.8% but larger top quark background as well (Figure 4.28). Because of this, the two channels have similar sensitivities to the $\mathrm{\text{H}}\mathrm{\text{H}}$ cross section.

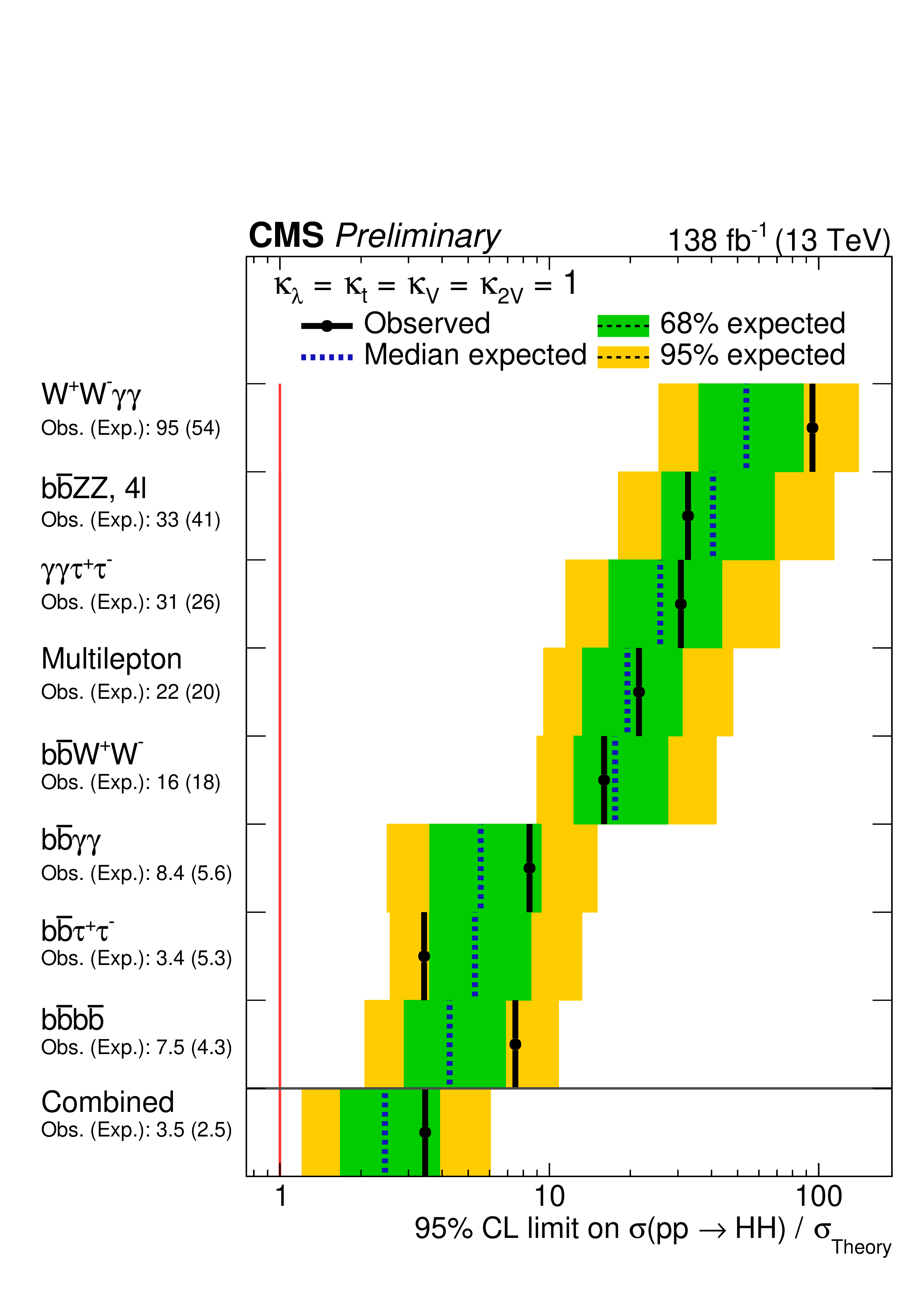
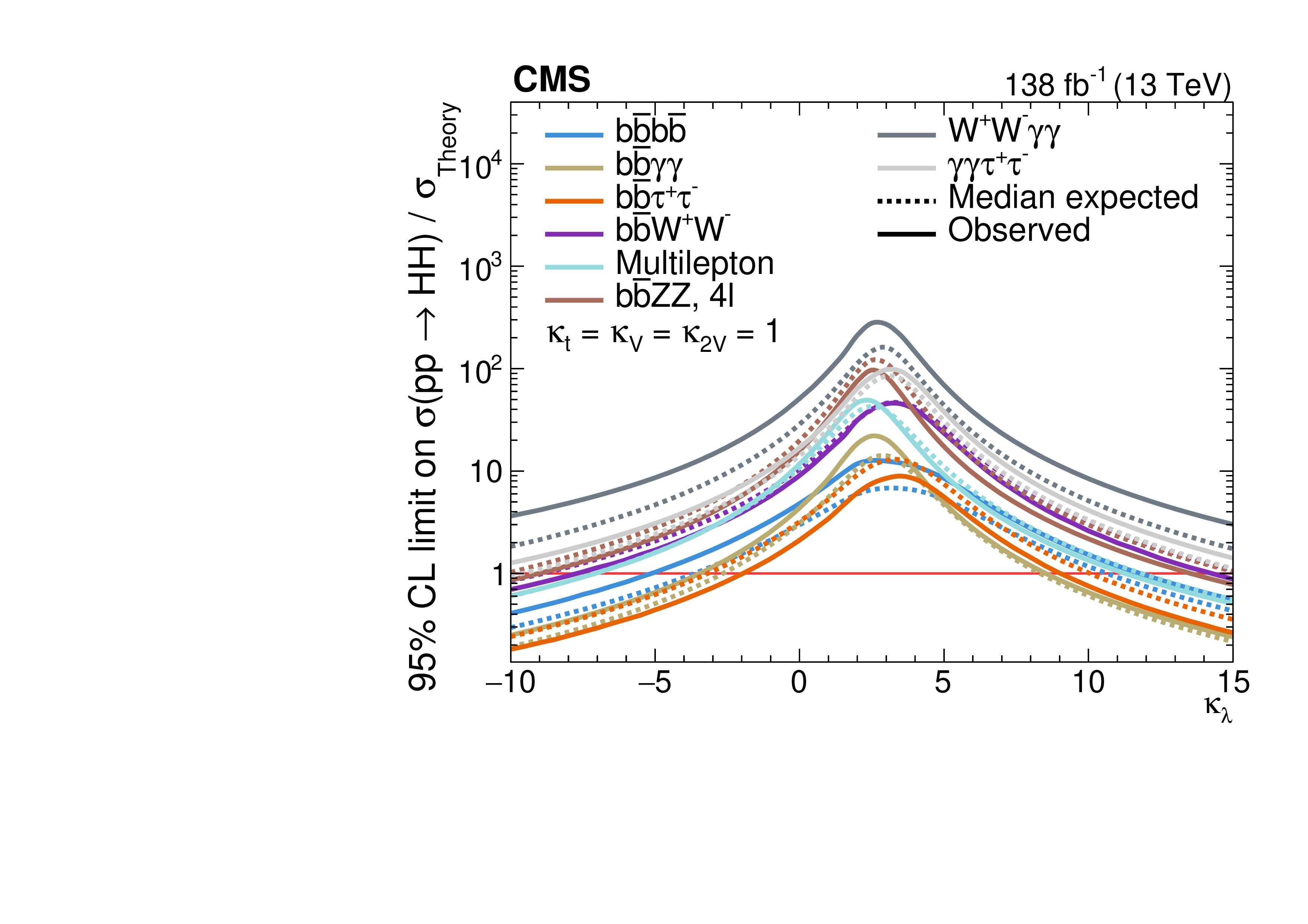
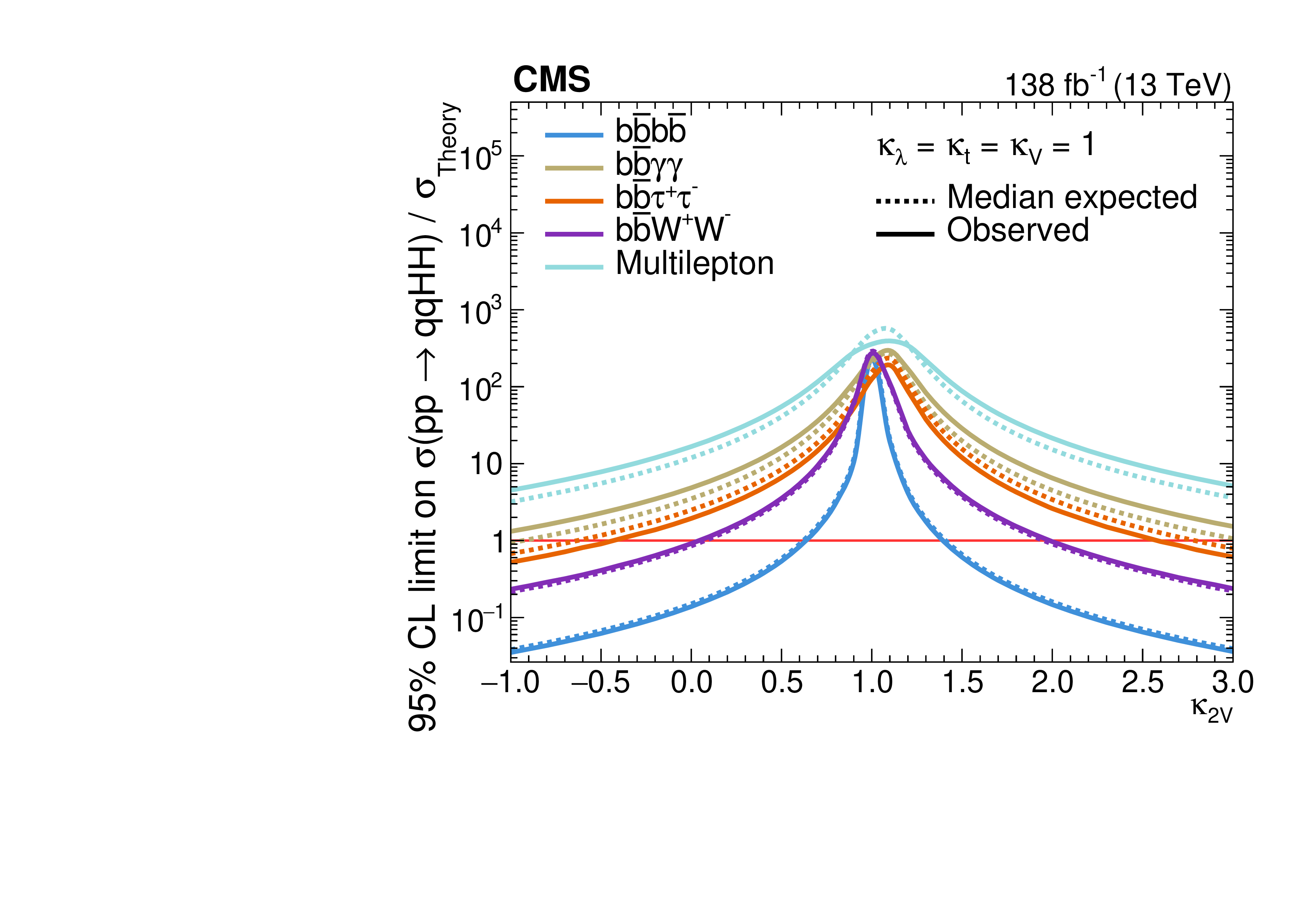
The limits set on the $\mathrm{\text{H}}\mathrm{\text{H}}$ cross section by each channel, and their combinations, are shown in Figure 4.29, and as a function of ${\kappa }_{\lambda }$ and ${\kappa }_{2\mathrm{\text{V}}}$ in Figure 4.30. The three “golden channels” each offer roughly similar sensitivities to the cross section and ${\kappa }_{\lambda }$ limits; however, the constraint on ${\kappa }_{2\mathrm{\text{V}}}$ is dominated by the boosted $\mathrm{\text{b}}\overline{\mathrm{\text{b}}}\mathrm{\text{b}}\overline{\mathrm{\text{b}}}$ channel, because of the enhancement of boosted $\mathrm{\text{H}}\mathrm{\text{H}}$ production at BSM ${\kappa }_{2\mathrm{\text{V}}}$ deviations, as discussed in Section 4.3.2. Its observed (expected) $95\%$ confidence level (CL) constraint is $[0.6,1.4]$ ($[0.7,1.4]$). This is followed by the resolved $\mathrm{\text{b}}\overline{\mathrm{\text{b}}}\mathrm{\text{b}}\overline{\mathrm{\text{b}}}$ [28] and $\mathrm{\text{b}}\overline{\mathrm{\text{b}}}\mathit{\tau \tau }$ [29] channels, with constraints of $[-0.1,2.2]$ ($[-0.4,2.5]$) and $[-0.4,2.6]$ ($[-0.6,2.8]$), respectively. Similarly, the strongest ${\kappa }_{2\mathrm{\text{V}}}$ constraint from the ATLAS experiment is from the recent boosted $\mathrm{\text{b}}\overline{\mathrm{\text{b}}}\mathrm{\text{b}}\overline{\mathrm{\text{b}}}$ search [163], with an observed (expected) $95\%$ CL constraint of $[0.55,1.49]$ ($[0.3,1.7]$).

In this dissertation, we present the first search for nonresonant $\mathrm{\text{H}}\mathrm{\text{H}}$ production in the all-hadronic $\mathrm{\text{b}}\overline{\mathrm{\text{b}}}\mathrm{\text{V}}\mathrm{\text{V}}$ channel, where one Higgs decays to two bottom quarks, while the other to two vector bosons ($\mathrm{\text{V}}\mathrm{\text{V}}$) both decaying hadronically to the four quark ($4\mathrm{\text{q}}$) final state. Both the W and Z bosons are considered for the latter decay and collectively referred to as V bosons. The branching fractions for the $\mathrm{\text{b}}\overline{\mathrm{\text{b}}}$ and $\mathrm{\text{V}}\mathrm{\text{V}}$ decays are $0.58$ and $0.25$ respectively, for a total branching fraction $B(\mathrm{\text{H}}\mathrm{\text{H}}\to \mathrm{\text{b}}\overline{\mathrm{\text{b}}}\mathrm{\text{V}}\mathrm{\text{V}})=2\cdot 0.58\cdot 0.25=0.29$, which is the second-highest, behind only $\mathrm{\text{b}}\overline{\mathrm{\text{b}}}\mathrm{\text{b}}\overline{\mathrm{\text{b}}}$. The all-hadronic final state in particular has a branching fraction of $0.13$. The analysis targets the boosted regime, which, as discussed above, has the two-fold advantage of 1) increasing sensitivity to ${\kappa }_{2\mathrm{\text{V}}}$ deviations and 2) exponentially reducing the dominant QCD multijet background.

4.3.4 BSM $\mathrm{\text{X}}\to \mathrm{\text{H}}\mathrm{\text{Y}}$ production

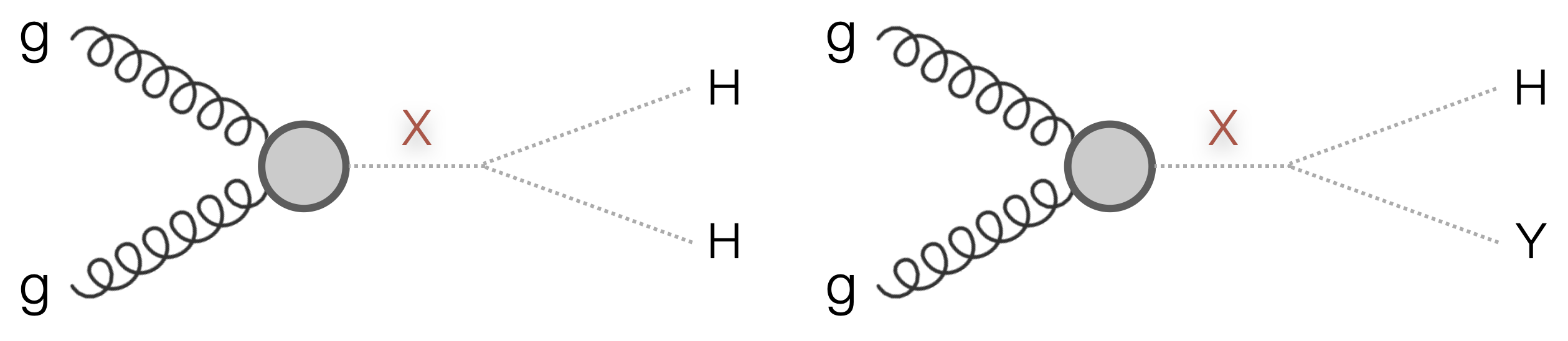
Many theoretical models predict a richer scalar sector than that in the SM to address aesthetic and observational inconsistencies with the SM, such as the Higgs mass hierarchy problem and the baryon asymmetry discussed above. These include two-Higgs doublet models (2HDM) [165] that add an additional scalar doublet to the SM, such as the minimal supersymmetric extension of the SM (MSSM) [153], which predicts two neutral CP-even scalars (H, h), one neutral CP-odd scalar (A), and two charged scalars (${\mathrm{\text{H}}}^{\pm }$), where one of the neutral CP-even scalars may be the discovered SM Higgs ${\mathrm{\text{H}}}_{125}$. The next-to-minimal supersymmetric extension of the SM (NMSSM) [166] adds to this a complex scalar singlet, predicting two more CP-even (${\mathrm{\text{h}}}_s$) and CP-odd (${\mathrm{\text{a}}}_s$) neutral scalars. Finally, the two-real-singlet-model (TRSM) predicts two additional CP-even scalar fields. Depending on the kinematics, all these models allow for cascade decays of a heavier scalar to symmetric and asymmetric lighter scalars, such as $\mathrm{\text{H}}\to {\mathrm{\text{H}}}_{125}{\mathrm{\text{H}}}_{125}$ and $\mathrm{\text{H}}\to \mathrm{\text{h}}{\mathrm{\text{H}}}_{125}$, respectively, as shown in Figure 4.31.

We search for this broad class of signals, looking for generic decays of the form $\mathrm{\text{X}}\to \mathrm{\text{H}}\mathrm{\text{Y}}$, where X is the heavier and Y the lighter scalar resonance, with H decaying to $\mathrm{\text{b}}\overline{\mathrm{\text{b}}}$ and Y to $\mathrm{\text{V}}\mathrm{\text{V}}\to 4\mathrm{\text{q}}$. Many models, such as the TRSM, predict branching ratios for the lighter scalar similar to or the same as the SM Higgs. In this case, the $\mathrm{\text{V}}\mathrm{\text{V}}$ decay modes are dominant for $m_Y>140\text{GeV}$ (Figure 4.18) and, hence, the $\mathrm{\text{H}}\to \mathrm{\text{b}}\overline{\mathrm{\text{b}}}$ and $\mathrm{\text{Y}}\to \mathrm{\text{V}}\mathrm{\text{V}}$ will be the dominant final states for the $\mathrm{\text{X}}\to \mathrm{\text{H}}\mathrm{\text{Y}}$ signal. Thus, the $\mathrm{\text{b}}\overline{\mathrm{\text{b}}}\mathrm{\text{V}}\mathrm{\text{V}}$ channel represents the highest BF in these models.

There are several published and ongoing CMS searches for $\mathrm{\text{X}}\to \mathrm{\text{H}}\mathrm{\text{Y}}$ production in a variety of regimes and final states with the Run 2 dataset, such as the boosted [167] $\mathrm{\text{b}}\overline{\mathrm{\text{b}}}\mathrm{\text{b}}\overline{\mathrm{\text{b}}}$ final state, the symmetric-only $\mathrm{\text{b}}\overline{\mathrm{\text{b}}}\mathrm{\text{W}}\mathrm{\text{W}}$ semi-leptonic final state [31], the resolved $\mathrm{\text{b}}\overline{\mathrm{\text{b}}}\mathit{\gamma \gamma }$ [168], and the resolved $\mathrm{\text{b}}\overline{\mathrm{\text{b}}}\mathit{\tau \tau }$ [169] final state. This dissertation presents the first search in the $\mathrm{\text{b}}\overline{\mathrm{\text{b}}}\mathrm{\text{V}}\mathrm{\text{V}}$ all-hadronic state, and the first in the $\mathrm{\text{b}}\overline{\mathrm{\text{b}}}\mathrm{\text{V}}\mathrm{\text{V}}$ state for the asymmetric case, representing a significant increase in the covered phase space for $\mathrm{\text{X}}\to \mathrm{\text{H}}\mathrm{\text{Y}}$ searches.

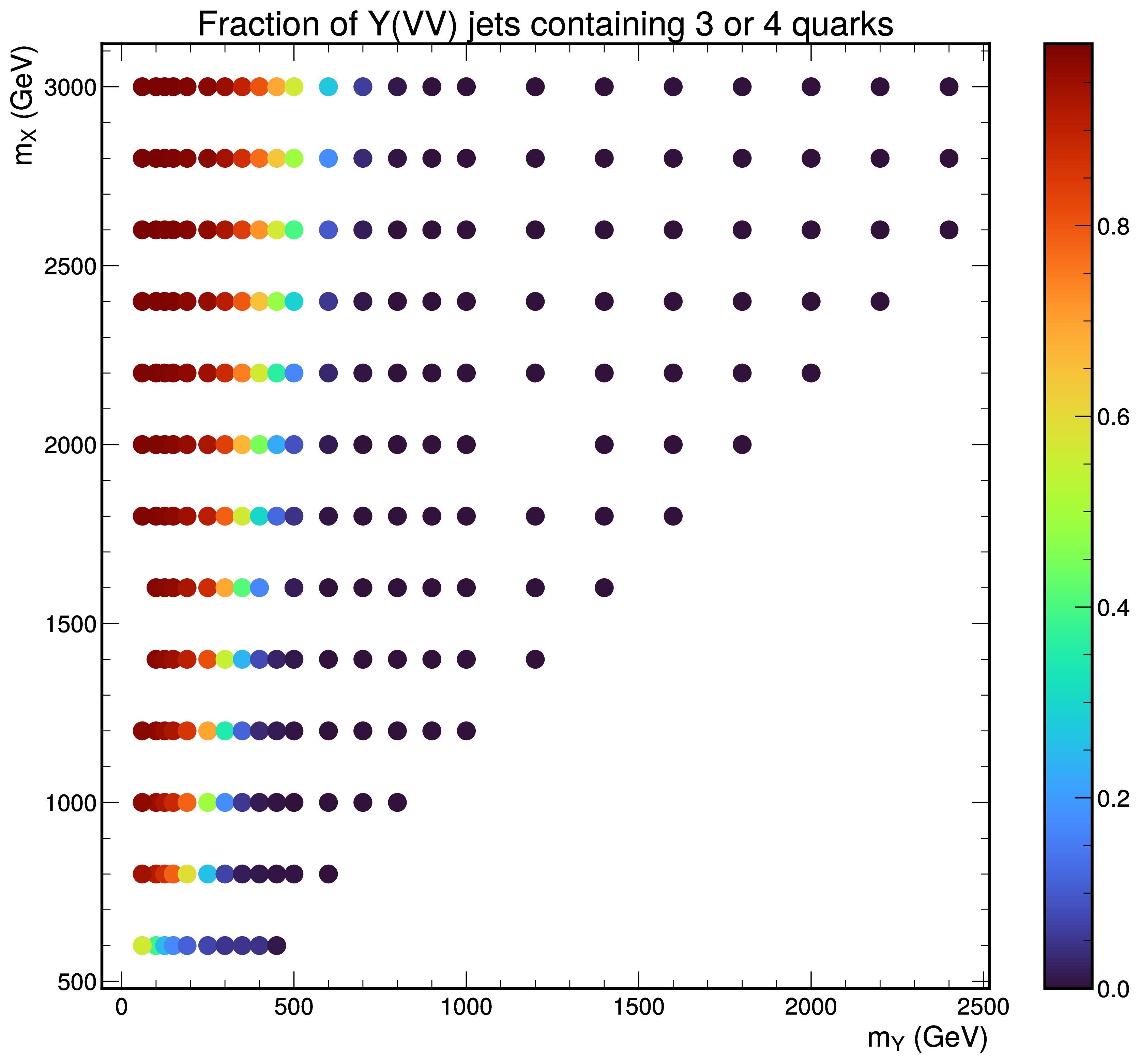
The search comprises two distinct topologies depending on the ratio of the X and Y masses: a highly-boosted fully-merged $\mathrm{\text{Y}}\to \mathrm{\text{V}}\mathrm{\text{V}}$ topology for $m_X\gg m_Y$, with both $\mathrm{\text{V}}\mathrm{\text{V}}$ bosons’ decay products highly collimated into a single wide-radius jet; and a relatively less-boosted semi-merged topology, where the $\mathrm{\text{V}}\mathrm{\text{V}}$ bosons are well separated and each $\mathrm{\text{V}}\to \mathrm{\text{q}}\mathrm{\text{q}}$ decay is reconstructed as its own wide-radius jet. These two phases are illustrated in Figure 4.32, showing the fraction of $\mathrm{\text{Y}}\to \mathrm{\text{V}}\mathrm{\text{V}}$ jets containing three or four generator-level quarks as a function of the X and Y boson masses, with the transition occurring around $m_X\approx 10m_Y$. This dissertation focuses on a search for the fully-merged topology only, i.e. for $m_X\gtrsim 10m_Y$, and is complementary to an ongoing CMS search in the semi-merged topology. Thus, in terms of the analysis strategy and techniques, this search is similar to the boosted nonresonant $\mathrm{\text{H}}\mathrm{\text{H}}$ search in that they both target highly-boosted Higgs boson decays with single wide-radius jets for both H or Y bosons.

Acknowledgements

Chapters 4.3.2 and 4.3.4 are in part, currently being prepared for the publication of the material by the CMS collaboration. The dissertation author was the primary investigator and author of these papers.