Electroweak interactions

4.2 Electroweak interactions

The weak interaction is the last of the three fundamental forces we discuss in the SM. Apart from its relatively weak coupling constant (Table 4.1), it is unique in several ways: (1) it couples only to left-chiral fermions, thereby violating parity ( $P$ ) and charge conjugation ( $C$ ); (2) it is the only force with massive gauge bosons, resulting in short-range interactions; and (3) it is the only force that “sees” and can change the flavors of the fermions. Hence, it is responsible for radioactive decays and the instability of all hadrons and leptons bar the proton and electron. Its couplings to the different flavors also lead to $CP$ -violation, as we discuss in Section 4.2.4.

4.2.1 Weak interactions

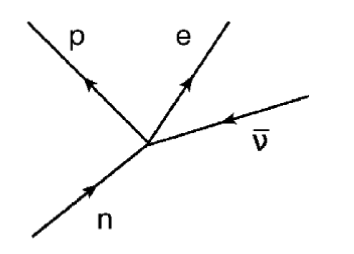
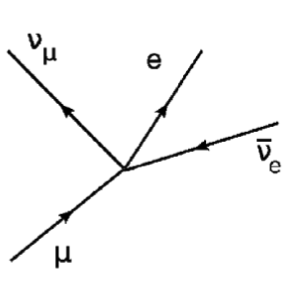
The first theory of weak interactions was Enrico Fermi’s 1933 theory of beta decay [143]: the decay of the neutron to a proton, $n \to p + e^{-} + {\bar{ν}}_{e}$ , through a four-fermion interaction (Figure 4.16, left). Fermi was inspired by Dirac’s nascent theory of QED, and using similar perturbative techniques, his theory proved successful in describing weak decays. The same principle was also applied to other weak decays, such as muon decay (Figure 4.16, right) and pion decay.

As it turned out, the four-fermion interaction is of mass dimension $6$ and not renormalizable (see Chapter 3.2), leading to the scattering cross-section diverging at high energies. This is, of course, because these interactions are in fact mediated by the massive weak $W^{\pm}$ and $Z$ gauge bosons, which become relevant around their mass scale of $O (100 GeV)$ . We now understand the Fermi theory as an effective field theory (EFT) valid for energies much lower than $100 GeV$ , wherein the $W$ and $Z$ boson DoFs can be integrated out and nonrenormalizable interactions are allowed — they are just suppressed by factors of ${(\frac{1}{M_{W}})}^{2}$ . This suppression is why the weak interaction is so weak, with a coupling constant of $\approx O (1 0^{- 6})$ at the mass scale of the proton.

Figure 4.16. Feynman diagrams for beta decay (left) and muon decay (right) in Fermi’s theory.

The weak interaction is described by an $SU (2)$ Yang-Mills theory, and is sometimes referred to as quantum flavordynamics (QFD) because of its deep connection to flavor, as we will discuss. However, “vanilla” Yang-Mills theories cannot accommodate massive gauge bosons; hence, it was only after the development of the ABEGHHK (Higgs) mechanism in the 1960s that this description gained traction. Specifically, Sheldon Glashow, Abdus Salam, Steven Weinberg and others showed that the spontaneous breaking of an $SU (2)$ $\times$ $U (1)$ symmetry to $U (1)$ could not only yield massive weak gauge bosons, but also naturally incorporate QED with a massless photon [113–115].

This combined electroweak theory has been experimentally confirmed in many stages: first with the discovery of neutral currents involving neutrinos with the Gargamelle bubble chamber at CERN in 1973 [144], the first evidence for the $Z$ boson (the only neutral boson that couples to neutrinos); then with the direct discovery of the $W$ and $Z$ bosons at the Super Proton Synchrotron (SPS) in 1983 [145–148], as well as precision measurements of electroweak parameters such as the $W$ and $Z$ masses with the Large Electron-Positron Collider (LEP) in the 1990s; and finally with the discovery of the Higgs boson at the LHC in 2012 [60, 149], a particle predicted by the ABEGHHK mechanism, and the ongoing measurements of its properties.

4.2.2 Before electroweak symmetry breaking

Electroweak interactions are associated with the $SU {(2)}_{L} \times U {(1)}_{Y}$ gauge symmetry, which is “spontaneously broken” to $U {(1)}_{EM}$ through the ABEGHHK mechanism during electroweak symmetry breaking (EWSB).⁵ We label the three gauge bosons of $SU {(2)}_{L}$ as $W^{1}, W^{2}, W^{3}$ and of $U {(1)}_{Y}$ as $B$ , with coupling constants $g$ and $g^{'}$ , respectively.

The fermions in the SM can be categorized by their representations, or charges, under the three gauge symmetries before EWSB, as in Table 4.2. The bold numbers indicate the dimension of the representation under the respective symmetry group, while the regular numbers are the charges under the $U {(1)}_{Y}$ group — referred to as their hypercharge, $Y$ .

------|--------------------------
|
|U (1 )Y SU (2)L SU (3)C
------|--------------------------
|
| 1
QL | + 6 2 3
|
| 1
LL | − 2 2 1
|
| 2
uR | + 3 1 3
|
| 1
dR | − 3 1 3
|
|
eR | − 1 1 1
|
|
νR? | 0 1 1
|
| 1
--H---|-+-2-------2--------1----- — Table 4.2. The representations and charges of fermionic and scalar fields in the SM under the $U {(1)}_{Y}$ , $SU {(2)}_{L}$ , and $SU {(3)}_{C}$ gauge symmetries. The right-handed neutrino is included here for completeness but has not been experimentally confirmed.

The weak interactions specifically are associated with the $SU {(2)}_{L}$ gauge symmetry, and their key characteristic is that they violate parity: they only couple to left-handed fermions and right-handed antifermions (hence, the subscript $L$ ). Specifically, the left-handed quarks ( $u_{L}$ and $d_{L}$ ) and leptons ( $ν_{L}$ and $e_{L}$ ) reside in $SU {(2)}_{L}$ doublets:

Q_{L} = (\begin{matrix} u_{L} \\ d_{L} \end{matrix}), L_{L} = (\begin{matrix} ν_{L} \\ e_{L} \end{matrix}),

(4.2.1)

while right-handed fermions live in the trivial representation. The $L$ and $R$ subscripts indicate left- and right-chiral Weyl spinors, respectively. Note that there are actually three generations of fermions, which we index as $u^{i}$ for $i = 1, 2, 3$ ; however, before EWSB, there is no distinction between them as they are all massless. Often, we will omit this index when the properties across generations are identical.

The SM also contains a scalar, $SU (2)$ -doublet “Higgs” field $H$ , which is listed in Table 4.2 as well. Its dynamics are governed by the Lagrangian:

L_{Higgs} = {(D_{μ} H)}^{†} (D^{μ} H) - λ {(H^{†} H - \frac{v^{2}}{2})}^{2},

(4.2.2)

where $v$ is a constant and

D_{μ} H = [\partial_{μ} - ig W_{μ} - \frac{i}{2} g^{'} B_{μ}] H

(4.2.3)

is the covariant derivative of $H$ . The potential resembles the sombrero potential from Figure 3.7, but with a 2D rather than 1D complex field.

The Higgs field is able to couple to the fermions without violating gauge symmetry through Yukawa interactions. The most general possible Yukawa terms are $3 \times 3$ matrices across the three generations.

L_{Yukawa} = - y_{ij}^{d} {\bar{Q}}_{L}^{i} H d_{R}^{j} - y_{ij}^{u} {\bar{Q}}_{L}^{i} \tilde{H} u_{R}^{j} - y_{ij}^{e} {\bar{L}}_{L}^{i} H e_{R}^{j} - y_{ij}^{ν} {\bar{L}}_{L}^{i} \tilde{H} ν_{R}^{j} + h.c.,

(4.2.4)

where $\tilde{H} = i σ_{2} H^{†}$ is the charge-conjugated Higgs field, $i$ and $j$ index the three generations of fermions, $y_{ij}^{d}$ are the Yukawa coupling constant matrices, and h.c. denotes the Hermitian conjugate of all the preceding terms.

The Higgs field contracts with the fermionic left-handed $SU (2)$ -doublets to produce an $SU (2)$ -singlet, while the quark fields contract with each other to form $SU (3)$ -singlets. One can also check that through our clever choice of $H$ vs. $\tilde{H}$ , the total hypercharge of each term is $0$ . Thus, each Yukawa term is independently gauge invariant.

The overall electroweak Lagrangian is:

\begin{matrix} L_{EW} = - \frac{1}{4} W_{μν}^{a} W^{aμν} - \frac{1}{4} B_{μν} B^{μν} \\ + {\bar{Q}}_{L} i D Q_{L} + {\bar{L}}_{L} i D L_{L} + ū_{R} i D u_{R} + {\bar{d}}_{R} i D d_{R} + ē_{R} i D e_{R} \\ + L_{Higgs} + L_{Yukawa}, & (4.2.5) \end{matrix}

Note that without EWSB, not only are all the gauge bosons of the theory massless, but so are the fermions: the usual fermionic mass terms of the form $m u_{L} u_{R}$ violate the $SU {(2)}_{L}$ gauge symmetry. As we will see, the ABEGHHK mechanism is what generates masses for all the fermions, through the Higgs Yukawa couplings, as well as the three weak gauge bosons.

4.2.3 Electroweak symmetry breaking

EWSB occurs when the Higgs field spontaneously breaks the global $SU {(2)}_{L} \times U {(1)}_{Y}$ symmetry by moving to a ground state of the potential. Without loss of generality, we can choose this ground state to be:

⟨ H ⟩ = \frac{1}{\sqrt{2}} (\begin{matrix} 0 \\ v \end{matrix}),

(4.2.6)

where $⟨ H ⟩$ is the vacuum expectation value (VEV) of the Higgs field. As before, we can parametrize the fluctuations around this ground state as:

H = e^{i ξ^{A} (x) T^{A}} \frac{1}{\sqrt{2}} (\begin{matrix} 0 \\ v + h (x) \end{matrix}),

(4.2.7)

where $h$ is a real scalar field, $T^{A}$ are three generators of the broken $SU {(2)}_{L} \times U {(1)}_{Y}$ symmetry, and $ξ^{A}$ are the corresponding Goldstone bosons.

The ABEGHHK mechanism for gauge theories effectively involves the original gauge bosons absorbing these Goldstone bosons, thereby acquiring mass (see Chapter 3.4). This can be equivalently thought of as simply a convenient choice of gauge in which $ξ^{A} (x) = 0$ . In the end, after some algebra, the gauge $+$ Higgs sector of the electroweak Lagrangian after EWSB looks like:

\begin{matrix} L_{GH} = - \frac{1}{4} W_{μν}^{a} W^{aμν} - \frac{1}{4} B_{μν} B^{μν} + \frac{1}{2} \partial_{μ} h \partial^{μ} h - \underset{\equiv V (h)}{\underset{⏟}{λ h^{2} {(v + \frac{h}{2})}^{2}}} \\ + \frac{1}{8} {(v + h)}^{2} [g^{2} {(W_{μ}^{1})}^{2} + g^{2} {(W_{μ}^{2})}^{2} + {(g W_{μ}^{3} - g^{'} B_{μ})}^{2}], & (4.2.8) \end{matrix}

where $V (h)$ is the new Higgs potential.

We now have mass terms for three gauge, as well as the Higgs, bosons. As always, we are free to define the gauge boson fields as we wish, and it turns out the most convenient choice is:

\begin{matrix} \begin{aligned} W_{μ}^{\pm} & = \frac{1}{\sqrt{2}} (W_{μ}^{1} \mp i W_{μ}^{2}), \\ Z_{μ} & = \frac{1}{\sqrt{g^{2} + {g^{'}}^{2}}} (g W_{μ}^{3} - g^{'} B_{μ}), \\ A_{μ} & = \frac{1}{\sqrt{g^{2} + {g^{'}}^{2}}} (g^{'} W_{μ}^{3} + g B_{μ}) . \end{aligned} \end{matrix}

(4.2.9)

It is conventional to define the Weinberg or weak mixing angle $𝜃_{W}$ :

\cos 𝜃_{W} = \frac{g}{\sqrt{g^{2} + {g^{'}}^{2}}}, \sin 𝜃_{W} = \frac{g^{'}}{\sqrt{g^{2} + {g^{'}}^{2}}},

(4.2.10)

to simplify the forms of $Z$ and $A$ above:

\begin{matrix} \begin{aligned} Z_{μ} & = W_{μ}^{3} \cos 𝜃_{W} - B_{μ} \sin 𝜃_{W}, \\ A_{μ} & = W_{μ}^{3} \sin 𝜃_{W} + B_{μ} \cos 𝜃_{W} . \end{aligned} \end{matrix}

(4.2.11)

Experimentally, we have determined the free parameters of this theory to be:

v \approx 250 GeV, λ \approx 0.35, g \approx 0.64, g^{'} \approx 0.34 \Rightarrow \sin^{2} 𝜃_{W} \approx 0.223,

(4.2.12)

at an energy scale of the $Z$ boson mass. The Lagrangian can hence be written as:

\begin{matrix} L_{GH} = - \frac{1}{4} W_{μν}^{+} W^{- μν} - \frac{1}{4} Z_{μν} Z^{μν} - \frac{1}{4} F_{μν} F^{μν} + m_{W}^{2} W_{μ}^{+} W^{- μ} + \frac{1}{2} m_{Z}^{2} Z_{μ} Z^{μ} \\ + \frac{2 m_{W}^{2}}{v} h W_{μ}^{+} W^{- μ} + \frac{m_{Z}^{2}}{v} h Z_{μ} Z^{μ} + \frac{m_{W}^{2}}{v^{2}} h^{2} W_{μ}^{+} W^{- μ} + \frac{m_{Z}^{2}}{4 v^{2}} h^{2} Z_{μ} Z^{μ} \\ + \frac{1}{2} \partial_{μ} h \partial^{μ} h - m_{h}^{2} h^{2} - λv h^{3} - \frac{1}{4} λ h^{4}, & (4.2.13) \end{matrix}

where

m_{W} = \frac{1}{2} vg \approx 80 GeV, m_{Z} = \frac{1}{2} v \sqrt{g^{2} + {g^{'}}^{2}} \approx 91 GeV, m_{h} = \sqrt{2 λ} v \approx 125 GeV .

(4.2.14)

Note that in addition to the gauge-boson self-interactions, the Higgs field also has a trilinear ( $λv h^{3}$ ) and quartic ( $\frac{1}{4} λ h^{4}$ ) self-interaction terms. While some manner of EWSB has been confirmed experimentally through the discovery of the Higgs boson, its full nature, and the full form of the Higgs potential, can only be determined through measurements of these terms. The trilinear self-coupling, in particular, can be accessed at the LHC through pair production of the Higgs boson, as we will discuss in Section 4.3. Higgs pair production also allows exclusive access to the quartic $hhV V$ couplings, where $V$ is a weak gauge boson.

The photon and re-emergence of Dirac spinors

$A_{μ}$ corresponds to the one unbroken symmetry of the original $SU {(2)}_{L} \times U {(1)}_{Y}$ group. In terms of the original generators — three $T^{A}$ s for $SU {(2)}_{L}$ and one $Y$ for $U {(1)}_{Y}$ — $A_{μ}$ corresponds to linear combination $Q = T^{3} + Y$ . This is the massless photon field, with the gauge group $U {(1)}_{EM}$ .

The eigenvalue of $Q$ for each fermion corresponds to their electric charge under this group. For the $SU {(2)}_{L}$ -singlet fields, $T_{3}$ has no value and hence $Q = Y$ , while for the doublets, $T_{3}$ has eigenvalues $\pm \frac{1}{2}$ for the upper and lower components, respectively: e.g. for $u_{L}$ , $Q = \frac{1}{2} + \frac{1}{6} = \frac{2}{3}$ and for $e_{L}$ , $Q = - \frac{1}{2} - \frac{1}{2} = 1$ . In the end, we see that the left- and right-chiral fermion field pairs have the same charge under this remaining unbroken symmetry, so they can again form Dirac spinors:

ψ_{u} = (\begin{matrix} u_{L} \\ u_{R} \end{matrix}), ψ_{d} = (\begin{matrix} d_{L} \\ d_{R} \end{matrix}), ψ_{e} = (\begin{matrix} e_{L} \\ e_{R} \end{matrix}), ψ_{ν} = (\begin{matrix} ν_{L} \\ ν_{R} \end{matrix}),

(4.2.15)

times three for each generation.

Each Weyl spinor pair interacts identically with the photon and gluons but the $W$ and $Z$ bosons continue to couple only to the left-handed components. For example the $W^{+}$ –fermion coupling is:

L_{W^{+} f} = - \frac{g}{\sqrt{2}} W_{μ}^{+} \underset{\equiv J_{μ}^{+}}{\underset{⏟}{(ū_{L} {\bar{σ}}^{μ} d_{L} + {\bar{ν}}_{L} {\bar{σ}}^{μ} e_{L})}},

(4.2.16)

where $J_{μ}^{+}$ is called the weak charged current. In terms of Dirac spinors, this can be written using the projection operator (Eq. B.4.13):

L_{W^{+} f} = - \frac{g}{\sqrt{8}} W_{μ}^{+} ({\bar{ψ}}_{u} γ^{μ} (1 - γ_{5}) ψ_{d} + {\bar{ψ}}_{ν} γ^{μ} (1 - γ_{5}) ψ_{e}) .

(4.2.17)

Recall that $\bar{ψ} γ^{μ} ψ$ is a Lorentz vector, while $\bar{ψ} γ^{μ} γ_{5} ψ$ is a pseudo- or axial-vector, so the weak current is effectively an axial vector subtracted from a vector. Indeed, historically, the weak interaction was referred to as “V-A” theory.

A hierarchy problem

Generally, if we encounter a new energy scale in nature, we are either able to connect it in some way to an existing scale or a (broken) symmetry of the theory. For example, the mass of the proton $\sim 1 GeV$ is based on the QCD confinement scale $Λ_{QCD} \sim 200 MeV$ , which in turn is related to the Planck scale $Λ_{Planck} \sim 1 0^{19} GeV$ through dimensional transmutation. The mass of the pion on the other hand, $\approx 140 MeV$ , is a consequence of chiral symmetry breaking in QCD. Physicists such as Dirac and Gell-Mann have in fact proposed these criteria as a principle of “naturalness” for physical theories [150, 151].

There are many examples of mysterious energy scales appearing experimentally, which were either later rationalized or in fact even used to correctly predict new physics, such as the prediction of the charm quark mass based on the small mass difference between the $K_{L}^{0}$ and $K_{S}^{0}$ mesons. The electroweak energy scale of $\approx 100 GeV$ is one such example which has yet to be explained.

A common way of expressing the problem is based on the Higgs mass: if we believe the SM to be an EFT valid up to some energy scale $Λ$ , and if we have a priori no other energy scale to which to tie the Higgs mass, then we expect higher order corrections to its bare mass to be of order $Λ$ . For example, if there is no new physics up to the Planck scale, then we are left with a bare mass and correction both of order $1 0^{19} GeV$ . The fact that the actual mass is $125 GeV$ implies a cancellation between the two, or finetuning, at a $\frac{125}{1 0^{19}} \approx 1 0^{- 15} %$ level. This is considered highly “unnatural” and is called a hierarchy problem, perhaps hinting at new physics.

One possibility is that $Λ$ is in fact on the order of the Higgs mass, and we are simply yet to find the new degrees of freedom at this $O (100 GeV)$ scale. Or, if we accept a higher level of finetuning, e.g. at the $10 %$ or $1 %$ levels, $Λ$ can be pushed up further to $1$ – $10 TeV$ . Effectively, we can invert the hierarchy problem into setting a bound on new physics!

Another solution is the existence an underlying (approximate) symmetry of nature “protecting” the Higgs mass from higher order corrections, similar to the chiral symmetry for the pion mass. The most promising candidate is supersymmetry, postulating an additional global symmetry between bosons and fermions [152]. Both these solutions possibly hint at an extended scalar sector, with either another Higgs doublet or new scalar singlets, for example, through the minimal supersymmetric extension of the SM (MSSM) [153] or based on two-real-scalar-singlet models [154]. This is one motivation behind the search for new Higgs bosons described in this dissertation. A more detailed, pedagogical discussion of naturalness can be found in e.g. Nathaniel Craig’s IAS lectures [155].

4.2.4 Fermion masses and flavor

After EWSB, we have

H = \frac{1}{\sqrt{2}} (\begin{matrix} 0 \\ v + h \end{matrix}), \tilde{H} = \frac{1}{\sqrt{2}} (\begin{matrix} v + h \\ 0 \end{matrix}),

(4.2.18)

which yields the following Yukawa Lagrangian:

L_{Yukawa} = - \frac{1}{\sqrt{2}} (v + h) [y_{ij}^{d} {\bar{d}}_{L}^{i} d_{R}^{j} + y_{ij}^{u} ū_{L}^{i} u_{R}^{j} + y_{ij}^{e} ē_{L}^{i} e_{R}^{j} + y_{ij}^{ν} {\bar{ν}}_{L}^{i} ν_{R}^{j}] + h.c. .

(4.2.19)

Again, we are free to redefine fields and can choose a basis for all the fermion fields in which the Yukawa matrices are diagonal:

u_{L}^{i} \to {(V^{u})}_{j}^{i} u_{L}^{j}, d_{L}^{i} \to {(V^{d})}_{j}^{i} d_{L}^{j}, u_{R}^{i} \to {(U^{u})}_{j}^{i} u_{R}^{j}, d_{R}^{i} \to {(U^{d})}_{j}^{i} d_{R}^{j},

(4.2.20)

such that

V^{† u} Y^{u} U^{u} = diag (m_{u}, m_{c}, m_{t}), V^{† d} Y^{d} U^{d} = diag (m_{d}, m_{s}, m_{b}),

(4.2.21)

and same for the leptons (though again with the caveat that the right-handed neutrino, $ν_{R}$ , has not been experimentally confirmed).

This is the mass eigenstate basis, where each generation and type of fermion has terms of the form:

L_{Yukawa} = - \frac{v}{\sqrt{2}} y^{u} ū_{L} u_{R} - \frac{h}{\sqrt{2}} y^{u} u_{L} u_{R} + h.c. + \dots,

(4.2.22)

i.e., a mass term $m_{X} = \frac{v y^{X}}{\sqrt{2}}$ and a Yukawa interaction term with the Higgs field of strength $y^{X}$ . The same Yukawa constant determines both the mass of the particle and its coupling to the Higgs field; indeed, in Appendix B.4.5, we show how this is used to determine the Higgs to fermion decay rates!

Like $v$ and $λ$ , the Yukawa couplings are all free parameters of the SM which can only be determined experimentally.

The CKM and PMNS matrices

Observe that the transformation we needed to diagonalize the Yukawa matrices in Eq. 4.2.20 violates the $SU {(2)}_{L}$ symmetry, by transforming the up and down components of $Q_{L}$ and $L_{L}$ independently. This is actually okay because the $SU {(2)}_{L}$ symmetry was already broken through EWSB; however, crucially, this means the weak eigenstates (also called the flavor eigenstates), which the W bosons couple together, are not the same as the mass eigenstates!

Explicitly, any term which couples the up or down components of the $SU (2)$ -doublet only with their respective right-handed components, such as the kinetic terms $\partial_{μ} u_{L} \partial^{μ} u_{L}$ or the electromagnetic interaction $A_{μ} {\bar{ψ}}_{u} γ^{μ} ψ_{L}$ , is invariant under the transformation in Eq. 4.2.20. It is only the weak charged currents (Eq. 4.2.16) in the SM which mix the two. Including the three generations, the positive current is:

J_{μ}^{+} = \sum_{i} ū_{L}^{i} {\bar{σ}}^{μ} d_{L}^{i} + \sum_{i} {\bar{ν}}_{L}^{i} {\bar{σ}}^{μ} e_{L}^{i}

(4.2.23)

in the flavor eigenstate basis (the negative current is simply the h.c.). But if we attempt to transform to the mass basis via Eq. 4.2.20:

J_{μ}^{+} = \sum_{i} ū_{L}^{i} {\bar{σ}}^{μ} \underset{\equiv V_{CKM}}{\underset{⏟}{{[{(V^{u})}^{†} V^{d}]}_{ij}}} d_{L}^{j} + \sum_{i} {\bar{ν}}_{L}^{i} {\bar{σ}}^{μ} \underset{\equiv V_{PMNS}}{\underset{⏟}{{[{(V^{ν})}^{†} V^{e}]}_{ij}}} e_{L}^{i},

(4.2.24)

we are left with these two matrices, called the Cabibbo-Kobayashi-Maskawa (CKM) [126] and Pontecorvo-Maki-Nakagawa-Sakata (PMNS) [156] matrices mixing the quark and lepton flavors, respectively. The upshot is that the $W$ bosons can not only mix the components of (the former) $SU {(2)}_{L}$ doublets, but also different mass eigenstates! The $Z$ and photon currents do not have this property, which is why we say there are no flavor-changing neutral currents (FCNCs) in the SM, at least at tree level.

The magnitude of this mixing by the $W$ s is determined by the CKM and PMNS matrices. They are $3 \times 3$ unitary matrices that, after accounting for the various constraints imposed by the fermion masses, unitarity, etc., have $4$ free parameters each. They are most often parametrized as three real Euler angles and one complex phase, which again have to be determined experimentally. Importantly, this complex phase means the weak interaction violates $CP$ -symmetry as well!

To see why, we can go back to the Yukawa interactions, this time with the hermitian conjugates included:

L_{Yukawa} \sim y_{ij}^{d} {\bar{d}}_{L}^{i} d_{R}^{j} + y_{ij}^{d *} {\bar{d}}_{R}^{i} d_{L}^{j} + \dots

(4.2.25)

One can check that the two field terms ${\bar{d}}_{L}^{i} d_{R}^{j}$ and ${\bar{d}}_{R}^{i} d_{L}^{j}$ are $CP$ -conjugates of each other, which means invariance under $CP$ requires $y_{ij}^{d} = y_{ij}^{d *}$ , i.e. the Yukawa matrix to be real. The complex phases in the CKM and PMNS matrices therefore lead to $CP$ -violation in the SM. Interestingly, for fewer than three generations, the two matrices cannot be imaginary. Kobayashi and Maskawa discovered this in 1973, after the observation of $CP$ -violation in 1964, and predicted a third generation of quarks to explain $CP$ -violation in the SM, for which they were awarded the Nobel prize in 2008.

Flavor is perhaps the least understood area of the SM: Why are their exactly three generations each of quarks and leptons? Why their particular hierarchy of masses? Is it a coincidence that nature chose the exact minimum number of generations needed to allow for $CP$ -violation? All of these mysteries point to the strong possibility of new physics in the flavor sector.

⁵As discussed in Chapter 3.4, technically, the gauge symmetry cannot be broken — what breaks is the associated global symmetry.