3.6 The ABEGHHK (Higgs) mechanism
As highlighted in the previous section, gauge bosons in pure Yang-Mills theories are massless. This is in conflict, however, with the short observed range of the weak force, implying massive mediatory bosons. To resolve this, a series of work in the early 1960s by Anderson, Brout, Englert, Guralnik, Hagen, Higgs, and Kibble (ABEGHHK) yielded a mechanism to give mass to the gauge bosons without violating gauge invariance [60–63], based on the concept of spontaneous symmetry breaking developed by Nambu [64, 65] and others.
By 1970, Glashow, Salam, Weinberg and others were able to use this mechanism to formulate a combined theory of weak and electromagnetic interactions, known as “electroweak” or Weinberg-Salam theory [66–68]. Electroweak unification has been one of the most significant breakthroughs in theoretical physics with several Nobel prizes cumulatively awarded for these developments.
In this section we outline the ABEGHHK mechanism — commonly (but reductively) referred to as the “Higgs mechanism” — first for an abelian gauge theory in Section 3.6.1 and then for non-abelian gauge theories 3.6.2 like the SM.
3.6.1 The abelian Higgs mechanism
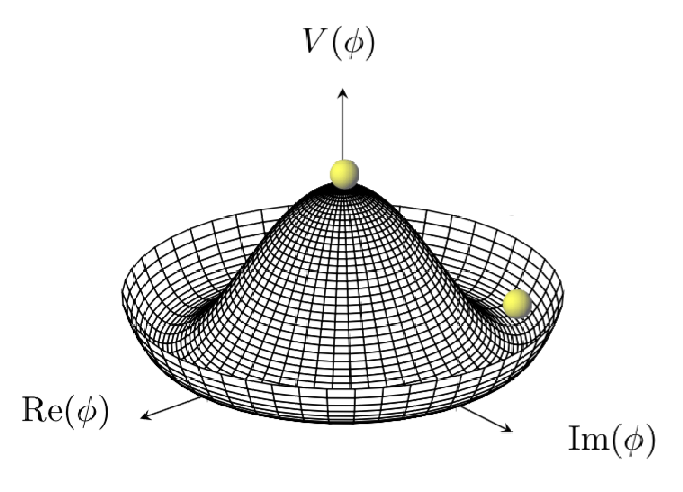
The Higgs mechanism is based on the idea of spontaneous symmetry breaking (SSB), where the ground states of a physical system violate the overall symmetry. The classic example is the so-called “sombrero” potential for a complex scalar field :
|
| (3.188) |
for constants and , shown in Figure 3.10. The potential has is symmetric under a transformation of , but any specific ground state of will break this symmetry, as shown in the figure. SSB is a crucial concept in physics, with several applications in condensed matter and particle physics, including chiral symmetry breaking in QCD (see e.g. Tong SM [5] Chapter 3.2).
The Higgs mechanism is an application of SSB to gauge symmetries. The interpretation here of SSB a bit fiddly since, as emphasized above, gauge symmetries are not physical and cannot be spontaneously broken;32 what actually breaks is the corresponding global symmetry, as we outline below.
Consider our QED Lagrangian for a complex scalar field with the above potential:
|
| (3.189) |
As before, this Lagrangian possesses a gauge symmetry; however, this symmetry is “broken” by a particular ground state (we can take WLOG). The fluctuations around the ground state can be parametrized as:
|
| (3.190) |
where and are two real fields. Plugging this into the Lagrangian gives us:
|
| (3.191) |
We see first that can be interpreted as a normal scalar quantum field, with a quadratic mass term with . The term is a bit more unusual;33 it only appears in the combination . Hence, we can simply redefine the gauge field as , allowing it to “absorb” this DoF. Note that this takes the form of a gauge transformation of and thus does not affect the field strength tensor . The resulting Lagrangian is then:
|
| (3.192) |
where we now have a mass term for the “gauge boson”, !
3.6.2 The non-abelian Higgs mechanism
There is an analogous mechanism for a non-abelian gauge symmetry, as in the SM. One crucial difference is that the symmetry may only partially break from the gauge group to a subgroup (for example from to a ). In this case, the gauge bosons corresponding to the generators of ’s broken symmetries acquire mass as above, while the generators of remain massless Goldstone bosons; as we will see in Chapter 4.2, in the SM these correspond to the massive / bosons and the massless photon, respectively. See e.g. Tong SM [5] Chapter 2.3.3 for an example.