Interactions

3.3 Interactions

Like the silicon chips of more recent years, the Feynman diagram was bringing computation to the masses. — Julian Schwinger

We next make the field theory more interesting by adding in interactions. We will continue with our scalar fields, first discussing the types of interactions that we will consider in Section 3.3.1. We then focus on weakly coupled theories, where we can treat the interactions as small perturbations, as described in Section 3.3.2, and then discuss how to calculate the probability of interactions occurring using Feynman diagrams in Section 3.3.3. Finally, we outline how to translate these probabilities into the physical quantities we measure, namely decay rates and cross sections, in Section 3.3.4.

3.3.1 Interactions in the Lagrangian

Before diving into the calculations, it is useful to get an idea of the types of interactions that are “relevant” in a QFT using dimensional analysis. Consider the following generic Lagrangian for a single real scalar field:

L = \frac{1}{2} \partial_{μ} ϕ \partial^{μ} ϕ - \frac{1}{2} m^{2} ϕ^{2} + \sum_{n = 3}^{\infty} \frac{λ_{n}}{n!} ϕ^{n} .

(3.67)

The $ϕ^{n}$ terms are what are new, representing interactions, and $λ_{n}$ are called their coupling constants, determining their respective strengths. Broadly speaking, we only know how to make meaningful analytic calculations for interactions which we can treat as small perturbations to the free Lagrangian; indeed, there is much we do not understand about strongly-coupled theories such as QCD.

How do we decide whether an interaction is “small”? It certainly depends on the coupling constant, but $λ$ is not necessarily dimensionless. The Lagrangian has energy (or mass) dimension 1 (using natural units, see Section 3.1.2), so

[L] = 4, [m] = 1 \Rightarrow [ϕ] = 1 \Rightarrow [\partial_{μ}] = 1, [λ_{n}] = 4 - n .

(3.68)

We need $λ$ to be small relative to different things, depending on its dimension. In fact, we use its dimension (or, equivalently, that of the interaction term) to categorize different interactions.

Relevant, marginal, and irrelevant interactions

$[λ_{3}] = 1$ : This means $λ_{3}$ must be small compared to some energy $E$ , which is typically the energy scale of our experiment or process of interest. Such an interaction therefore becomes a larger perturbation at lower energies, and smaller at high energies. These terms are called relevant because they affect the physics that we usually deal with.

$[λ_{4}] = 0$ : These are called marginal interactions, which are small if $λ_{4} ≪ 1$ .

$[λ_{n}] < 0, n > 4$ : These interactions are small at low energies and large at high energies. Because of this, we typically do not need to consider them in a QFT; hence, they are called irrelevant. Thus, in a sense, QFT is quite simple — we need only consider relevant and marginal interactions! In this case, $λ_{3} ϕ^{3}$ and $λ_{4} ϕ^{4}$ . The same dimensional analysis also shows why we do not consider terms with more than two derivatives.

When we do want to explore the effects of irrelevant interactions, we can parametrize them as generic operators in the Lagrangian which are suppressed by powers of ${(E ∕ Λ)}^{n - 4}$ , where $Λ$ is the energy scale at which we expect these interactions to become relevant. This is (one of) the ideas behind effective field theory (EFT) [28, 29].

Renormalizability

The types of interactions present in a theory also determine its renormalizability. Calculations in QFT are inherently plagued by infinities, one of which we encountered as the zero-point energy of the quantized free scalar field (Section 3.2.2). A general method for handling ultraviolet (UV) infinities — those which arise from integrating over momenta up to $| p | \to \infty$ — is to impose a cut-off energy scale $Λ$ on these integrals.

By doing so, we are essentially admitting, rightfully so, that we do not know what is going on arbitrarily high energies; hence, we do not expect our theory to be valid beyond $Λ$ . We then, after performing the integrals, can take the limit $Λ \to \infty$ and hope and pray our result is independent of $Λ$ . This is a simplified picture of renormalization.

However, the strength of irrelevant interactions only grows with energy, so $Λ \to \infty$ will lead to a divergence. Hence, we call theories with irrelevant interactions non-renormalizable. The SM is a renormalizable QFT and thus, as for our simple scalar field theory, its possible interactions are helpfully constrained. Most likely, it is simply an EFT of a higher energy theory, with the nonrenormalizable terms heavily suppressed by the scale of new physics!

3.3.2 S-matrix elements

As discussed above, we will focus on interactions in weakly-coupled theories, where they can be treated as small perturbations to the free Lagrangian. The quantized interaction terms comprise different combinations of creation and annihilation operators, corresponding to existing particles interacting, getting destroyed, and/or creating new ones. Broadly, we call these scattering processes, and the amplitude of these occurring is called the S-matrix element $⟨ f | S | i ⟩$ between the initial and final particles states $| i ⟩$ and $| f ⟩$ . The operator $S$ , for scattering, is called the S-matrix.

Note that so far we have only been discussing the abstract notion of fields in the Lagrangian. We have highlighted many connections and interpretations relating fields to physical particles, but they are not the same; fields are not particles.⁷ The S-matrix elements between particles are the physical quantities we measure: they are the basic observables of QFT.

Formally, fields and particles are related through the LSZ reduction formula [30], which expresses S-matrix elements in terms of the Green functions of the field (Section 3.2.5). The formula states that the S-matrix element between $n$ incoming and $m$ outgoing asymptotically free, on-shell particles is the residue of the $n + m$ particle pole of the associated fields’ Green functions.⁸

This is a very powerful result in QFT but, stated this way, not particularly useful for calculations... Instead, in this section, we heuristically explain the more practical consequence of the LSZ formula, which is that the S-matrix element can be calculated using the time-ordered product of the interacting fields, up to different orders in the interaction coupling constant. In the following section, we then present the even more practical method of calculating such time ordered products using Feynman diagrams.

Scalar Yukawa Lagrangian

We will use scalar Yukawa theory as an example, which couples together our real and complex scalar fields, $ϕ$ and $ψ$ :

L = \frac{1}{2} \partial_{μ} ϕ \partial^{μ} ϕ - \frac{1}{2} m^{2} ϕ^{2} + \partial_{μ} ψ^{†} \partial^{μ} ψ - M^{2} ψ^{†} ψ - gϕ ψ^{†} ψ .

(3.69)

The interaction term $gϕ ψ^{†} ψ$ is called a Yukawa interaction, and the weak coupling condition is $g ≪ m, M$ .

A similar theory was originally developed by Hideki Yukawa to model the strong nuclear force between nucleons ( $ψ$ ) via a hypothesized meson ( $ϕ$ ) [31]. Amazingly, such a meson was discovered a decade later via cosmic rays, and is called the pion [32]. Nobel Prizes were awarded for both the prediction and discovery. The difference in our theory is the scalar rather than fermionic nucleon, for simplicity; we will still, however, be able to reproduce the iconic physical feature of the theory: the Yukawa potential.

The interaction picture and Dyson’s formula

For treating interactions that are small perturbations to the free theory, it is most useful to employ the interaction picture of QM, a hybrid of the Schrödinger and Heisenberg pictures. Recall that in the Schrödinger picture, operators are fixed while states evolve with time, and vice versa in the Heisenberg picture. In the interaction picture, we split the Hamiltonian into the free ( $H_{0}$ ) and interaction terms ( $H_{int}$ ), defining operators to evolve with the former and states with the latter.

The upshot of this in QFT is that the S-matrix element can be written according to Dyson’s formula:

⟨ f | S | i ⟩ = ⟨ f | T \exp (- i \int_{- \infty}^{\infty} H_{I} (t) dt) | i ⟩,

(3.70)

where $T$ is the same time-ordering operator from Section 3.2.5 and $H_{I}$ is the time-evolved interaction Hamiltonian in the interaction picture:

H_{I} (t) = e^{i H_{0} t} H_{int} e^{- i H_{0} t} .

(3.71)

Assuming a small $H_{int}$ , Dyson’s formula can be Taylor expanded as:

\begin{matrix} ⟨ f | S | i ⟩ = ⟨ f | 𝟙 | i ⟩ + (- i) \int_{- \infty}^{\infty} ⟨ f | H_{I} (t) | i ⟩ dt \\ + \frac{{(- i)}^{2}}{2} \int \int_{- \infty}^{\infty} ⟨ f | T H_{I} (t_{1}) H_{I} (t_{2}) | i ⟩ d t_{1} d t_{2} + \dots . & (3.72) \end{matrix}

The first term in the expansion is the free field term, which we ignore.⁹ The $n$ th term after that is of order $g^{n}$ , where $g$ is the coupling constant of the interaction term. Thus, this offers a prescription for calculating the S-matrix element up to any fixed order in the interaction strength.

Note that $| i ⟩$ and $| f ⟩$ are particle momentum eigenstates of the free theory. We can justify this intuitively by thinking of them as the states long before and after the interaction, when the interaction term is negligible. Formally, there is in fact a complicated formula relating the free and interacting eigenstates; however, the proportionality factors cancel rather beautifully in the S-matrix element, allowing us to focus on only “connected” and “amputated” Feynman diagrams between the free eigenstates, which we define in the next section. This is illustrated (literally) for the vacuum states in Peskin and Schroeder [10] Chapter 4, and justified more generally by the LSZ reduction formula.

First-order examples and the matrix element $M$

Let us look at the $n = 1$ and $n = 2$ S-matrix element terms from Eq. 72 for our scalar Yukawa theory (Eq. 3.69):

\begin{matrix} \begin{aligned} {⟨ f | S | i ⟩}^{(1)} & = - i \int_{- \infty}^{\infty} ⟨ f | H_{I} (t) | i ⟩ dt = - ig \int d^{4} x ⟨ f | ϕ (x) ψ^{†} (x) ψ (x) | i ⟩, \\ {⟨ f | S | i ⟩}^{(2)} & = \frac{{(- ig)}^{2}}{2} \int d^{4} x \int d^{4} y ⟨ f | Tϕ (x) ψ^{†} (x) ψ (x) ϕ (y) ψ^{†} (y) ψ (y) | i ⟩ . \end{aligned} \end{matrix}

(3.73)

For given initial and final $N$ -particle momentum states, these can be calculated manually by plugging in the field expansions (Eq. 3.42 and 3.56). For example, the first-order term ${⟨ f | S | i ⟩}^{(1)}$ is non-zero only for processes like:

Meson decay $ϕ \to ψ^{†} ψ$ : $| i ⟩ = \sqrt{2 E_{p}} a_{p}^{†} | 0 ⟩$ , $| f ⟩ = \sqrt{4 E_{q_{1}} E_{q_{2}}} b_{q_{1}}^{†} c_{q_{2}}^{†} | 0 ⟩$ ; and
Nucleon-antinucleon annihilation $ψ^{†} ψ \to ϕ$ : $| i ⟩ = \sqrt{4 E_{q_{1}} E_{q_{2}}} b_{q_{1}}^{†} c_{q_{2}}^{†} | 0 ⟩$ , $| f ⟩ = \sqrt{2 E_{p}} a_{p}^{†} | 0 ⟩$ .

The amplitude for these can be calculated to be:

{⟨ f | S | i ⟩}^{(1)} = - ig {(2 π)}^{4} δ^{(4)} (p - q_{1} - q_{2}) .

(3.74)

The delta function ensures momentum conservation, and is in fact a general feature of all S-matrix elements. It also tells us that this process can only occur for $m \geq 2 M$ . We typically define

⟨ f | S - 𝟙 | i ⟩ \equiv i {(2 π)}^{4} δ^{(4)} (Σ p) M,

(3.75)

where $M$ is called the matrix element of the process, and is the nontrivial component we must compute.

For our first-order processes, we obtain the simple matrix element $M = - g$ . Generally, however, calculating $M$ each time using the field expansions can be quite cumbersome. This is especially true at higher orders, which require Wick’s theorem [33] to treat time-ordered fields. We can avoid this by using Feynman diagrams, and their associated rules, which allow us to simply read off a matrix element from a drawing of the process.

3.3.3 Feynman diagrams

Feynman diagrams are intuitive and powerful tools for calculating S-matrix elements. Examples for our first-order meson decay and nucleon-antinucleon annihilation processes are shown in Figure 3.1. They encode a lot of information (some of which is redundant, shown only for these first diagrams for clarity). Let us walk through some conventions we are using:

1.: Time and momentum always flow from left to right. Thus, the left-most particles represent the initial, and the right-most the final states. Momentum arrows are shown here explicitly but henceforth need not be.
2.: Mesons are plotted as dotted and nucleons as solid lines.
3.: Nucleon lines have arrows representing particle-flow. For external (i.e., initial or final state) nucleons they point in the direction of momentum for particles and opposite for antiparticles. Again, for future diagrams, particles need not be explicitly labeled as the linestyles and particle-flow arrows suffice.

†
ϕψψpqq12 — Figure 3.1: Feynman diagrams for meson decay (left) and nucleon-antinucleon annihilation (right).

ψϕψq1q2p† — Figure 3.1: Feynman diagrams for meson decay (left) and nucleon-antinucleon annihilation (right).

We can build up Feynman diagrams for higher-order processes by adding more vertices and internal lines connecting the vertices. As discussed above, only connected and amputated diagrams contribute to the S-matrix element, and we will focus on these. Connected means that every part of the diagrams is connected to at least one external line, and amputated means that there are no loops on external lines. Examples of disconnected and un-amputated diagrams are shown in Figure 3.2. Interestingly, disconnected and un-amputated diagrams contribute to the vacuum and one-particle states, respectively, differing in the interacting versus free theory.

Figure 3.2: Examples of a disconnected (left) and an un-amputated (right) Feynman diagram.

Feynman rules for scalar Yukawa theory

To read off the matrix element from a Feynman diagram, we take the product of factors associated to each element of the diagram, according to the Feynman rules of the theory. These rules are ultimately derived from and encode all our information about the underlying Lagrangian. They can be written in either position or momentum space; since we are working with momentum eigenstates, we will use the latter.

Definition 3.1. For our scalar Yukawa theory, the Feynman rules for calculating $i M$ are:¹⁰

1.: Vertices: $= - ig$
2.: Internal lines (propagators)
Mesons: $= \frac{i}{p^{2} - m^{2} + i𝜀}$ Nucleons: $= \frac{i}{q^{2} - M^{2} + i𝜀}$
3.: Impose momentum conservation at each vertex.
4.: Integrate over the momentum $k$ flowing through each loop $\int \frac{d^{4} k}{{(2 π)}^{4}}$ .

Note that the factors associated with internal lines are exactly the Feynman propagators from Section 3.2.5, which is in line with their interpretation as the amplitude for a particle to propagate from one point to another. For internal lines, the convention is for momentum to flow in the same direction as the particle flow, even for antiparticles. We discuss loops briefly at the end of this section; however, we focus primarily in this part on tree-level diagrams, those without loops.

We see immediately that these rules reproduce the matrix element $M = - g$ for our first-order processes, as expected. We next look at some more complicated, higher order diagrams.

Nucleon scattering

We start with nucleon-nucleon scattering $ψψ \to ψψ$ . The lowest order at which this can occur is of $O (g^{2})$ , as it requires at least two interaction vertices. The possible second-order diagrams are shown in Figure 3.3. We interpret them as nucleons interacting via the exchange of a meson. As the nucleons are identical, we require two diagrams, for the two permutations of the two final states.

kqiqiqfqf1212 — Figure 3.3: The two lowest order nucleon scattering diagrams.

kqiqiqfqf1221 — Figure 3.3: The two lowest order nucleon scattering diagrams.

Using the first two Feynman rules, we find

i M = {(- ig)}^{2} \cdot \frac{1}{k^{2} - m^{2} + i𝜀}

(3.76)

for both diagrams. What remains is to enforce momentum conservation at each vertex. For the left-most diagram, we see $k = q_{f 1} - q_{i 1} = q_{f 2} - q_{i 2}$ , while for the right-most $k = q_{f 2} - q_{i 1} = q_{f 1} - q_{i 2}$ . Thus, the total matrix element is

i M = i (M_{left} + M_{right}) = {(- ig)}^{2} [\frac{1}{{(q_{f 1} - q_{i 1})}^{2} - m^{2}} + \frac{1}{{(q_{f 2} - q_{i 1})}^{2} - m^{2}}],

(3.77)

where we have left out the $i𝜀$ term as there is no integral to perform.

Generally, we have to be careful with the relative signs of the matrix elements of different diagrams, corresponding to either constructive or destructive interference. (In fact, Peskin and Schroeder list “Figure out the overall sign of the diagram” as a Feynman rule.) In this case, we can reason physically that since nucleons are bosons, the amplitude will be symmetric under interchange of the two final states, and hence the two diagrams should be summed.

Virtual particles Note that by momentum conservation, the exchange meson does not have mass $m$ , as $k^{2} \neq m^{2}$ . We say that this meson is a virtual particle and is off-shell (referring to the “mass shell” in $k$ at $k^{2} = m^{2}$ ). This may appear dangerously unphysical; however, we are saved by the fact that such off-shell particles always appear internally in the diagram and thus can never be observed. In a sense, they can be viewed simply as a mathematical convenience in QFT. No one knows their correct physical interpretation; to quote Hong Liu, “In physics, when we don’t understand something, we give it a name and then claim we understand it.” [12].

Mandelstam variables

Because these types of 2-by-2 scattering processes are so common in particle physics, they have standard names, based on the momenta in the denominator of the matrix element.

Definition 3.2. For incoming particle momenta $p_{i 1}$ and $p_{i 2}$ and outgoing momenta $p_{f 1}$ and $p_{f 2}$ , the Mandelstam variables are defined as:

\begin{matrix} \begin{aligned} s & = {(p_{i 1} + p_{i 2})}^{2} = {(p_{f 1} + p_{f 2})}^{2}, \\ t & = {(p_{i 1} - p_{f 1})}^{2} = {(p_{i 2} - p_{f 2})}^{2}, \\ u & = {(p_{i 1} - p_{f 2})}^{2} = {(p_{i 2} - p_{f 1})}^{2} . \end{aligned} \end{matrix}

(3.78)

We can see that the matrix elements for nucleon scattering (Eq. 3.77) can be rewritten in terms of $t$ and $u$ as:

\begin{matrix} \begin{aligned} i M_{left} = {(- ig)}^{2} \cdot \frac{1}{t - m^{2}}, \\ i M_{right} = {(- ig)}^{2} \cdot \frac{1}{u - m^{2}} . \end{aligned} \end{matrix}

(3.79)

Hence, they are referred to as $t$ -channel and $u$ -channel diagrams, respectively. We will see an example of an $s$ -channel diagram in the next example. To build some intuition for these variables, let us sit in the center of mass (COM) frame, and define our coordinate frame such that incoming particles collide along the $z$ -axis and scatter in the $y$ - $z$ plane:

\begin{matrix} \begin{aligned} p_{i 1} = (E, 0, 0, p) & p_{i 2} = (E, 0, 0, - p) \\ p_{f 1} = (E, 0, p \sin 𝜃, p \cos 𝜃) & p_{f 2} = (E, 0, - p \sin 𝜃, - p \cos 𝜃) . \end{aligned} \end{matrix}

(3.80)

Then,

s = 4 E^{2}, t = - 2 p^{2} (1 - \cos 𝜃), u = - 2 p^{2} (1 + \cos 𝜃) .

(3.81)

Thus, $s$ is the total energy in the COM frame squared — hence, we usually refer to the COM energy as $\sqrt{s}$ — while $t$ and $u$ are a measure of how much momentum is exchanged between the scattered particles. For example, if $𝜃 = 0$ , both particles continue in the same direction and $t = 0$ , while if $𝜃 = π$ , they completely reverse direction and the momentum transfer along the collision axis is maximized at $\sqrt{| t |} = 2 p$ .

Nucleon-antinucleon scattering and resonances

Another interesting example is nucleon-antinucleon scattering $ψ ψ^{†} \to ψ ψ^{†}$ . At lowest order, we have the diagrams shown in Figure 3.4. Now, these are two distinct particles, so we do not have the $u$ -channel diagram with the final states interchanged as above. However, we do have a new $s$ -channel diagram on the right.

kqqqqiiff1212 — Figure 3.4: The two lowest order nucleon-antinucleon scattering diagrams.

Again, the first two Feynman rules result in the same matrix element (Eq. 3.76) for both. Imposing momentum conservation we find:

\begin{matrix} \begin{aligned} i M = i (M_{left} + M_{right}) & = {(- ig)}^{2} [\frac{1}{{(q_{f 1} - q_{i 1})}^{2} - m^{2}} + \frac{1}{{(q_{i 1} + q_{i 2})}^{2} - m^{2}}] . \\ = {(- ig)}^{2} (\frac{1}{t - m^{2}} + \frac{1}{s - m^{2}}) \end{aligned} \end{matrix}

(3.82)

Note an important point about the right matrix element, and $s -$ channel diagrams in general: the amplitude diverges as $s \to m^{2}$ .¹¹ Or, in other words, as the COM energy approaches the mass of the exchanged particle (as long as $m > 2 M$ ).

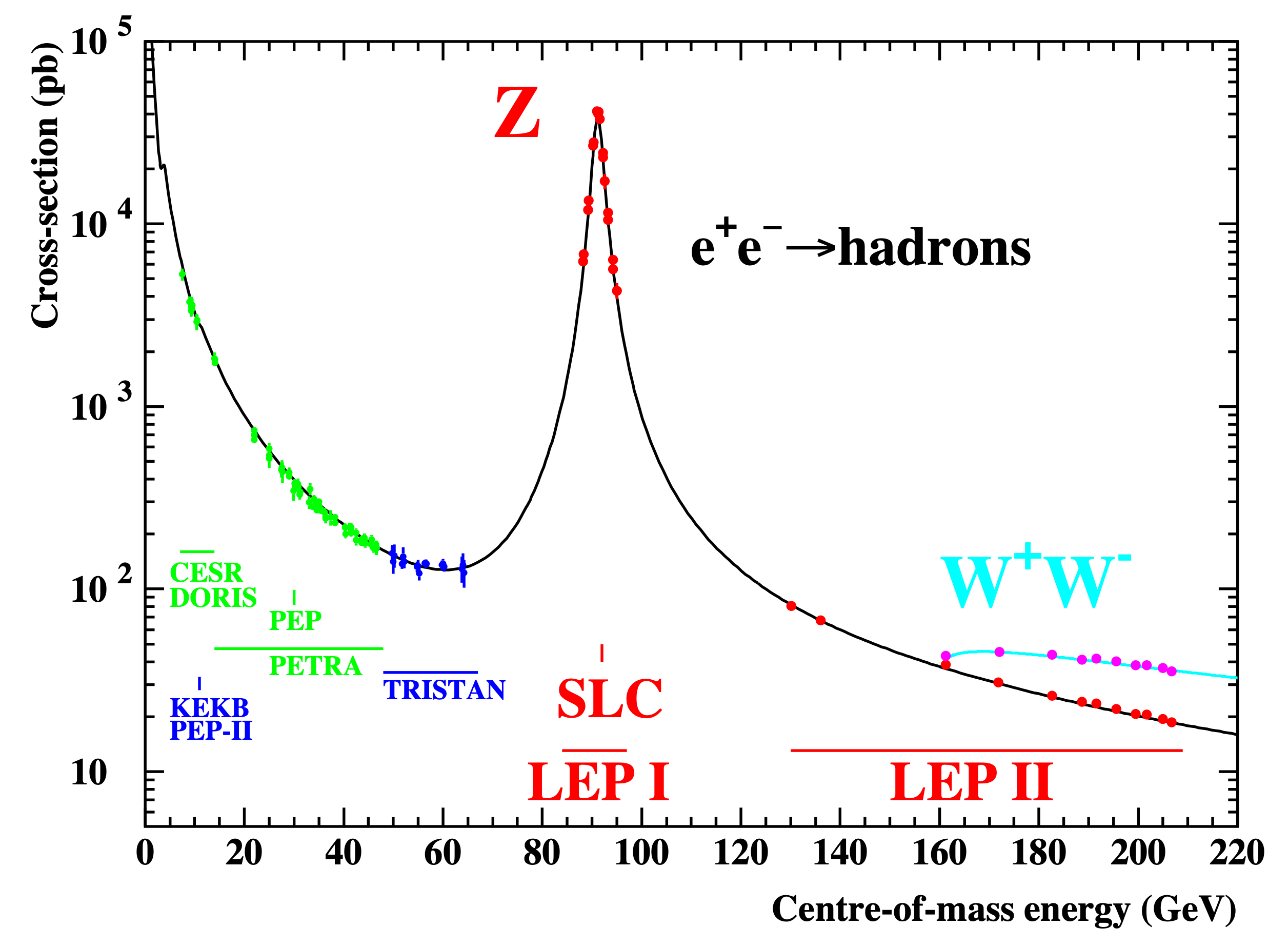
This divergence is interpreted as a resonance in the cross section (see below) of the scattering process as a function of $\sqrt{s}$ , and allows us to discover new particles. Figure 3.5 shows a great example for $e^{+} e^{-} \to$ hadron scattering by a series of HEP experiments with a magnificent peak at 96 $GeV$ , the $Z$ boson mass.

Figure 3.5: Cross section for $e^{+} e^{-} \to$ hadron scattering as a function of $\sqrt{s}$ with a clear resonance at the $Z$ boson mass, reproduced from Ref. [34].

The classical limit and the Yukawa potential

It is important to check our QFT recovers classical physics in the appropriate limit. It will also be useful to translate the somewhat abstract idea of amplitudes to the familiar concepts of forces and potentials. We will do so by considering the nonrelativistic limit ( $| p | ≪ M$ ) of our above amplitudes and using the Born approximation relating the scattering amplitude between two particles to the potential between them $U (r)$ :

M = ⟨ p_{f} | U (r) | p_{i} ⟩ = - i \int U (r) e^{i (p_{f} - p_{i}) \cdot r} d^{3} r,

(3.83)

where $r$ is the displacement between the particles.

First, let us consider what this potential would be classically. The static Klein-Gordon equation for a delta-function source:

(\nabla^{2} - m^{2}) ϕ (r) = δ^{3} (r),

(3.84)

can be found via the Fourier transform to be:

ϕ (r) = \frac{e^{- mr}}{4 πr} .

(3.85)

We can interpret this to be the profile of $ϕ$ around a nucleon (the delta function source), and thus conversely the potential felt by another nucleon via the meson and the Yukawa interaction, under the assumption $M ≫ m$ . This is entirely analogous to gauge potential $A_{0}$ in electrostatics generated by a $δ$ -function source acting as the electric potential for a test charge.

Going back to our amplitude for nucleon-antinucleon scattering, the $s$ -channel diagram vanishes in the nonrelativistic limit (which essentially means it does not have a simple classical interpretation), while the $t$ -channel diagram actually stays the same:

i M = - {(- ig)}^{2} \cdot \frac{1}{{| p_{f} - p_{i} |}^{2} - m^{2}} .

(3.86)

Plugging this into the LHS of Eq. 3.83 and inverting the RHS integral gives us:

U (r) = - \frac{g^{2}}{4 M^{2}} \cdot \frac{e^{- mr}}{4 πr} .

(3.87)

This is exactly the classical potential we found in Eq. 3.85! It is weighted by the coupling constant $g$ and $M$ to get the correct dimensions, and with a minus sign telling us potential is attractive.

Thus, we are able to reproduce Newtonian forces from the nonrelativisict limit of QFT. We also have the new interpretation of forces as simply manifestations of interactions in the Lagrangian, occurring through the exchange of virtual particles.

This potential is called the Yukawa potential, describing a force mediated by a massive boson. As expected, in the limit $m \to 0$ , we recover the familiar $1 ∕ r$ Coulomb potential, which is mediated by the massless photon. We can check that we obtain the same potential for nucleon-nucleon scattering and, more generally, that all forces mediated by scalars are attractive. In fact, this is true for spin-2 particles as well, which is why gravity is universally attractive! On the other hand, forces mediated by spin-1 particles, such as EM, can be either attractive or repulsive, with the charges of the particles involved determining the sign of each diagram. See e.g. Zee QFT [9] Chapter I.5 for a useful discussion.

Fourth-order diagrams and loops

So far, we have only considered tree-level diagrams, the simplest to calculate. This is in contrast to diagrams with loops, which can occur at higher order in perturbation theory. For example, at fourth-order we can have diagrams like those in Figure 3.6 for nucleon scattering.

Such diagrams contribute integrals over the loop momentum $k$ to the matrix element, which can notoriously diverge. To deal with this requires a process called renormalization, which, briefly, involves defining a cut-off energy scale $Λ$ for these integrals, beyond which we claim the theory is invalid. Experimentally, the main consequence is that physical parameters like the mass of particles and coupling constants in fact depend on the energy scale at which they are measured!

kkqiqiqfqfk1312122 — Figure 3.6: An example of a higher-order scattering diagram with a “loop”.

3.3.4 Decay rates and cross sections

In this section, we translate our S-matrix elements to physical observables: cross sections and decay rates.

Cross section

Classically for a scattering experiment, the number of particles scattered $N$ is related to the cross sectional area $σ$ as:

N = σT Φ,

(3.88)

where $T$ is the total time and $Φ$ is the flux of incoming particles (number of incoming particles per unit area and unit time). In QM, we define the cross section $σ$ similarly, but in terms of the probability of scattering $P$ instead of $N$ :

σ = \frac{P}{Φ T} .

(3.89)

This is a more abstract quantity in QM, but it still has units of area. The number of scattering events $N$ is related to $σ$ by a factor we call the luminosity $L$ :

N = σL .

(3.90)

Here, we simply consider this the definition of luminosity, but for a collider, for example, it can be derived from the properties of the input particle beams. Often, we are interested in the differential cross section $dσ$ with respect to kinematic variables like the solid angle $Ω$ or energy, so we write:

dσ = \frac{dP}{Φ T} .

(3.91)

As in QM, this probability $P$ is proportional to the square of the amplitude $| ⟨ f | S | i ⟩ |^{2}$ :

dP = \frac{{| ⟨ f | S | i ⟩ |}^{2}}{⟨ f | f ⟩ ⟨ i | i ⟩} d Π,

(3.92)

where $⟨ f | f ⟩$ and $⟨ i | i ⟩$ are the normalization factors for the final and initial states (they are not equal to $1$ as discussed in Section 3.2.5), and $d Π$ is the differential region of final state momenta.

For the case of two incoming particles (which is what is most relevant in collider physics), we can put all of this together to obtain the relation between differential cross section and the matrix element $M$ :

dσ = \frac{1}{(2 E_{1}) (2 E_{2}) | v_{1} - v_{2} |} {| M |}^{2} d Π_{LIPS},

(3.93)

where $E_{1}$ and $E_{2}$ are the energies of the incoming particles, $v_{1}$ and $v_{2}$ are their velocities, and $d Π_{LIPS}$ is called the Lorentz-invariant phase space of the final state momenta:

d Π_{LIPS} = {(2 π)}^{4} δ^{(4)} (Σ p) \prod_{final states j} \frac{d^{3} p_{j}}{{(2 π)}^{3}} \frac{1}{2 E_{j}}

(3.94)

For the case of $2 \to 2$ scattering, in the COM frame, this simplifies considerably:

(\frac{dσ}{d Ω})_{CM} = \frac{1}{64 π^{2} E_{CM}^{2}} \frac{| p_{f} |}{| p_{i} |} {| M |}^{2} 𝜃 (E_{CM} - m_{3} - m_{4}),

(3.95)

and even more so when the all four masses are equal:

(\frac{dσ}{d Ω})_{CM} = \frac{1}{64 π^{2} E_{CM}^{2}} {| M |}^{2} .

(3.96)

For nucleon-nucleon scattering in the COM frame, for example, we have (at tree level):

\begin{matrix} \begin{aligned} (\frac{dσ (𝜃)}{d Ω})_{CM} & = \frac{g^{4}}{64 π {(2 E)}^{2}} {(\frac{1}{t - m^{2}} + \frac{1}{u - m^{2}})}^{2} \\ = \frac{g^{4}}{64 π {(2 E)}^{2}} {[\frac{1}{2 p^{2} (1 - \cos 𝜃) - m^{2}} + \frac{1}{2 p^{2} (1 + \cos 𝜃) - m^{2}}]}^{2}, \end{aligned} \end{matrix}

(3.97)

where we used the expressions for $t$ and $u$ for a collision along the z-axis from Eq. 3.81.

Decay rate

The other type of process we are interested in are decays. The decay rate $Γ$ is simply the probability of decay per unit time:

Γ = \frac{P}{T} .

(3.98)

Using our expression for $P$ from above and simplifying, we find:

d Γ = \frac{1}{2 m} {| M |}^{2} d Π_{LIPS},

(3.99)

in the rest frame of the decaying particle, where $m$ is its mass. If multiple decays of the same particle are possible, we sum over the final states in the phase space integral. The total $Γ$ is then called the width of the particle, and $1 ∕ Γ \equiv τ$ is its half-life.

For our simple meson decay $ϕ \to ψ^{†} ψ$ , we have at tree level:

d Γ = \frac{g^{2}}{2 m} d Π_{LIPS} \Rightarrow Γ = \frac{g^{2}}{32 πm} {(1 - \frac{4 M^{2}}{m^{2}})}^{1 ∕ 2},

(3.100)

where we performed the integral over $d Π_{LIPS}$ (see Ref. [35] 4.2). This is in fact not too far off the expression for the decay width of the Higgs boson to fermions. What we are missing of course is that fermions are spin- $\frac{1}{2}$ particles, and we need to sum over their spin states. We will derive the correct expression (at tree level) in the next section.

⁷This point is well emphasized in Aneesh Manohar’s notes on EFT [28].

⁸Useful discussions of this can be found in Peskin and Schroeder [10] Chapter 7 and Schwartz [16] Chapter 6.

⁹Often we simply define the “interesting” part as $⟨ f | S - 𝟙 | i ⟩ \equiv iT$ and focus on calculating $T$ .

¹⁰These are derived nicely in Peskin and Schroeder [10] Chapter 4.7, albeit with fermionic electrons instead of our scalar “nucleons”.

¹¹We are saved from this potential infinity by a factor to be added to the denominator due to meson decay (Tong SM [5] Chapter 3.5).