10.1 Message passing GANs

In this chapter we describe two novel generative models for fast simulations of particle clouds in HEP. We first introduce the message-passing generative adversarial network (MPGAN) trained on high-energy JetNet jets. To our knowledge, it was the first generative model in HEP to effectively simulate point cloud data, and represented a breakthrough in the performance of ML-based fast simulations, leveraging sparse and efficient representations naturally suited to our data. It builds on top of the success of graph neural networks (GNNs) in learning from point clouds in computer vision, but is designed to take advantage of additional key inductive biases in HEP data, such as the non-local correlations between particles in a jet and their varying cardinalities.

The landscape of point cloud generative models in HEP and computer vision at the time of MPGAN’s publication was detailed in Chapter 7.3.3. In this section, we first discuss evaluation metrics used to compare MPGAN to existing models (Section 10.1.1) before describing the model architecture (Section 10.1.2). We then discuss experimental results, first on MNIST handwritten digits as a testbench in Section 10.1.3, and finally on the JetNet dataset in Section 10.1.4.

10.1.1 Evaluation

Evaluating generative models is a difficult task; however, there has been extensive work in this area in both the physics and computer-vision communities. We provide here a brief overview of the metrics used for comparing MPGAN and the baseline models discussed above, leaving a more detailed discussion, as well as an introduction to the novel metrics we develop for this task, to Chapter 11.

Physics-inspired metrics

An accurate jet simulation algorithm should reproduce both low-level and high-level features (such as those described in Chapter 7.3.3); hence, a standard method of validating generative models, which we too employ, is to compare the distributions of such features between the real and generated samples [279–283, 321].

For application in HEP, a generative model needs to produce jets with physical features indistinguishable from real. Therefore, we propose the validation criteria that differences between real and generated sample features may not exceed those between sets of randomly chosen real samples. To verify this, we use bootstrapping to compare between random samples of only real jets as a baseline.

A practically useful set of features to validate against are the so-called “energy-flow polynomials” (EFPs) [322], which are a type of multi-particle correlation functions. Importantly, the set of all EFPs forms a linear basis for all experimentally useful — i.e., all infrared- and colinear- (IRC-) safe — jet-level features / observables. Therefore, we claim that if we observe all EFP distributions to be reproduced with high fidelity and to match the above criteria, we can conclude with strong confidence that our model is outputting accurate particle clouds.

Computer-vision-inspired metrics

A popular metric for evaluating images which has been shown to be sensitive to output quality and mode-collapse — though it has its limitations [323] — is the Fréchet Inception Distance [324] (FID). FID is defined as the Fréchet distance between Gaussian distributions fitted to the activations of a fully-connected layer of the Inception-v3 image classifier in response to real and generated samples. We develop a particle-cloud-analogue of this metric, which we call Fréchet ParticleNet Distance (FPND), using the state-of-the-art (SOTA) ParticleNet graph convolutional jet classifier [230] in lieu of the Inception network. We note that FPND and comparing distributions as above are conceptually equivalent, except here instead of physically meaningful and easily interpretable features, we are comparing those found to be statistically optimum for distinguishing jets.

Two common metrics for evaluating point cloud generators are coverage (COV) and minimum matching distance (MMD) [296]. Both involve finding the closest point cloud in a sample $X$ to each cloud in another sample $Y$, based on a metric such as the Chamfer distance or the earth mover’s distance. Coverage is defined as the fraction of samples in $X$ which were matched to one in $Y$, measuring thus the diversity of the samples in $Y$ relative to $X$, and MMD is the average distance between matched samples, measuring the quality of samples. We use both, and due to drawbacks of the Chamfer distance pointed out in Ref. [296], for our distance metric choose only the analogue of the earth mover’s distance for particle clouds a.k.a. the energy mover’s distance (EMD) [325]. We discuss the effectiveness and complementarity of all four metrics in evaluating clouds in Section 10.1.4..

10.1.2 Architecture

We describe now the architecture of the MPGAN model (Figure 10.1), noting particle-cloud-motivated aspects compared to its r-GAN and GraphCNN-GAN predecessors (see Chapter 7.3.3).

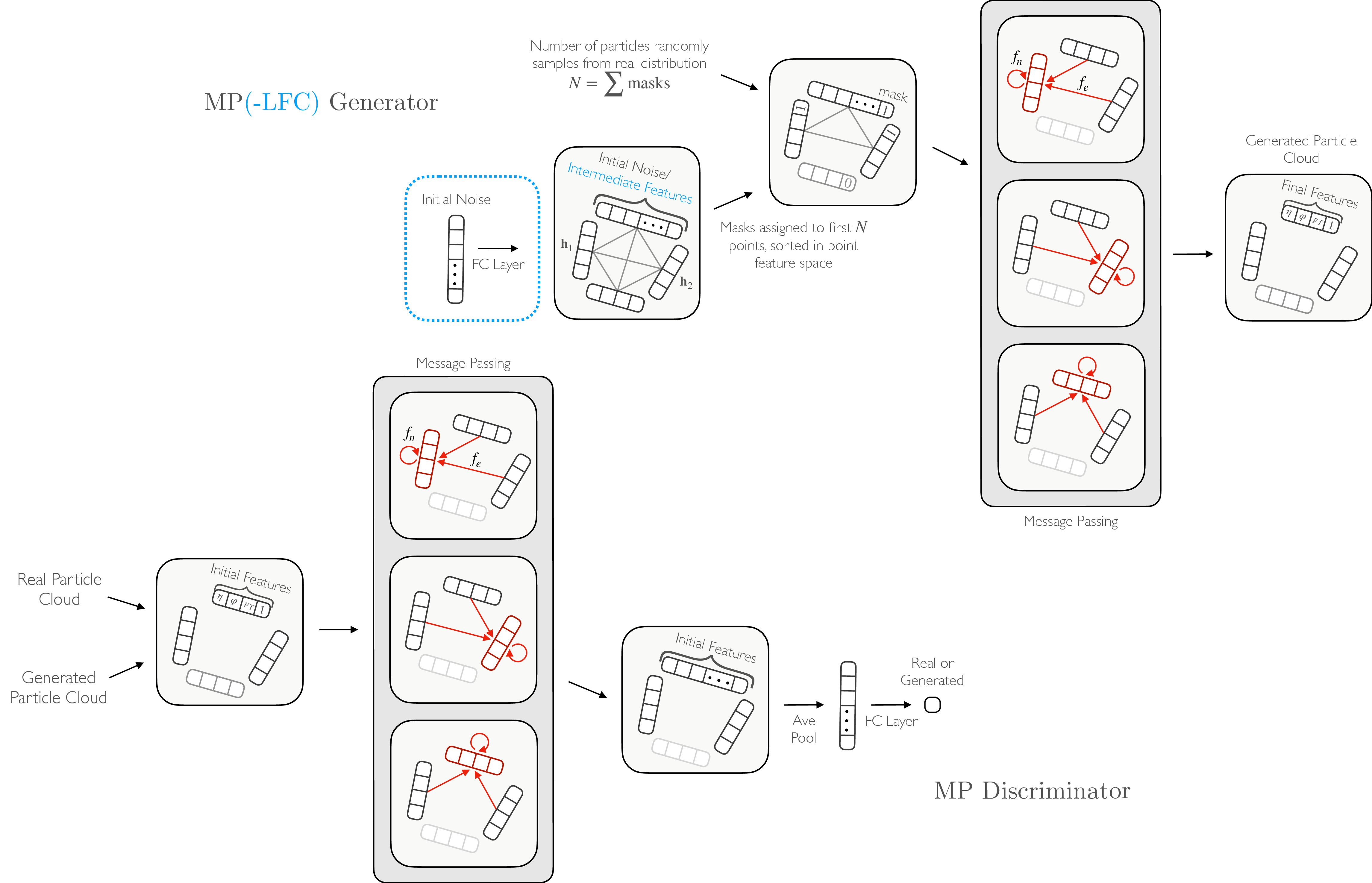
Message passing

Jets originate from the decay and hadronization of a single source-particle; hence, they end up with important high-level jet features and a rich global structure, known as the jet substructure [326], stemming from the input particle. Indeed, any high-level feature useful for analyzing jets, such as jet mass or multi-particle correlations, is necessarily global [322]. Because of this, while past work in learning on point clouds [230, 327, 328], including GraphCNN-GAN, has used a locally connected graph structure and convolutions for message passing, we choose a fully connected graph, equally weighting messages from all particles in the clouds. Rather than subtracting particle features for messages between particles, useful in graph convolutions to capture local differences within a neighborhood, the respective features are concatenated to preserve the global structure (the difference between particle features is also only physically meaningful if they are in the 4-vector representation of the Lorentz group). During the update step in the message passing we find it empirically beneficial to incorporate a residual connection to previous particle features.

The operation can be described as follows. For an $N$-particle cloud $J^t=\{p_1^t,\cdots ,p_N^t\}$ after $t$ iterations of message passing, with $t=0$ corresponding to the original input cloud, each particle $p_i^t$ is represented by features $h_i^t$. One iteration of message passing is then defined as

where $m_{\mathit{ij}}^{t+1}$ is the message vector sent from particle $j$ to particle $i$, $h_i^{t+1}$ are the updated features of particle $i$, and $f_e^{t+1}$ and $f_n^{t+1}$ are arbitrary functions which, in our case, are implemented as multilayer perceptrons (MLPs) with 3 FC layers.

Generator

We test two initializations of a particle cloud for the MPGAN generator: (1) directly initializing the cloud with $N$ particles, each with $L$ randomly sampled features, which we refer to as the MP generator, and (2) inputting a single $Z$-dimensional latent noise vector and transforming it via an FC layer into an $N\times L$-dimensional matrix, which we refer to as the MP-Latent-FC (MP-LFC) generator. MP-LFC uses a latent space which can intuitively be understood as representing the initial source particle’s features along with parameters to capture the stochasticity of the jet production process. Due to the complex nature of this process, however, we posit that this global, flattened latent space cannot capture the full phase space of individual particle features. Hence, we introduce the MP generator, which samples noise directly per particle, and find that it outperforms MP-LFC (Table 10.2).

Discriminator

We find the MP generator, in conjunction with a PointNet discriminator, to be a significant improvement on every metric compared to FC and GraphCNN generators. However, the jet-level features are not yet reproduced to a high enough accuracy (Section 10.1.4.). While PointNet is able to capture global structural information, it can miss the complex interparticle correlations in real particle clouds. We find we can overcome this limitation by incorporating message passing in the discriminator as well as in the generator. Concretely, our MP discriminator receives the real or generated cloud and applies MP layers to produce intermediate features for each particle, which are then aggregated via a feature-wise average-pooling operation and passed through an FC layer to output the final scalar feature. We choose 2 MP layers for both networks.

Variable-sized clouds

In order to handle clouds with varying numbers of particles, as typical of jets, we introduce an additional binary “masking” particle feature classifying the particle as genuine or zero-padded. Particles in the zero-padded class are ignored entirely in the message passing and pooling operations. The MP generator adds mask features to the initial particle cloud, using an additional input of the size of the jet $N$, sampled from the real distribution per jet type, before the message passing layers, based on sorting in particle feature space. Ablation studies with alternative (as well as without) masking strategies are discussed in Appendix C.1.3.

10.1.3 Experiments on MNIST handwritten digits

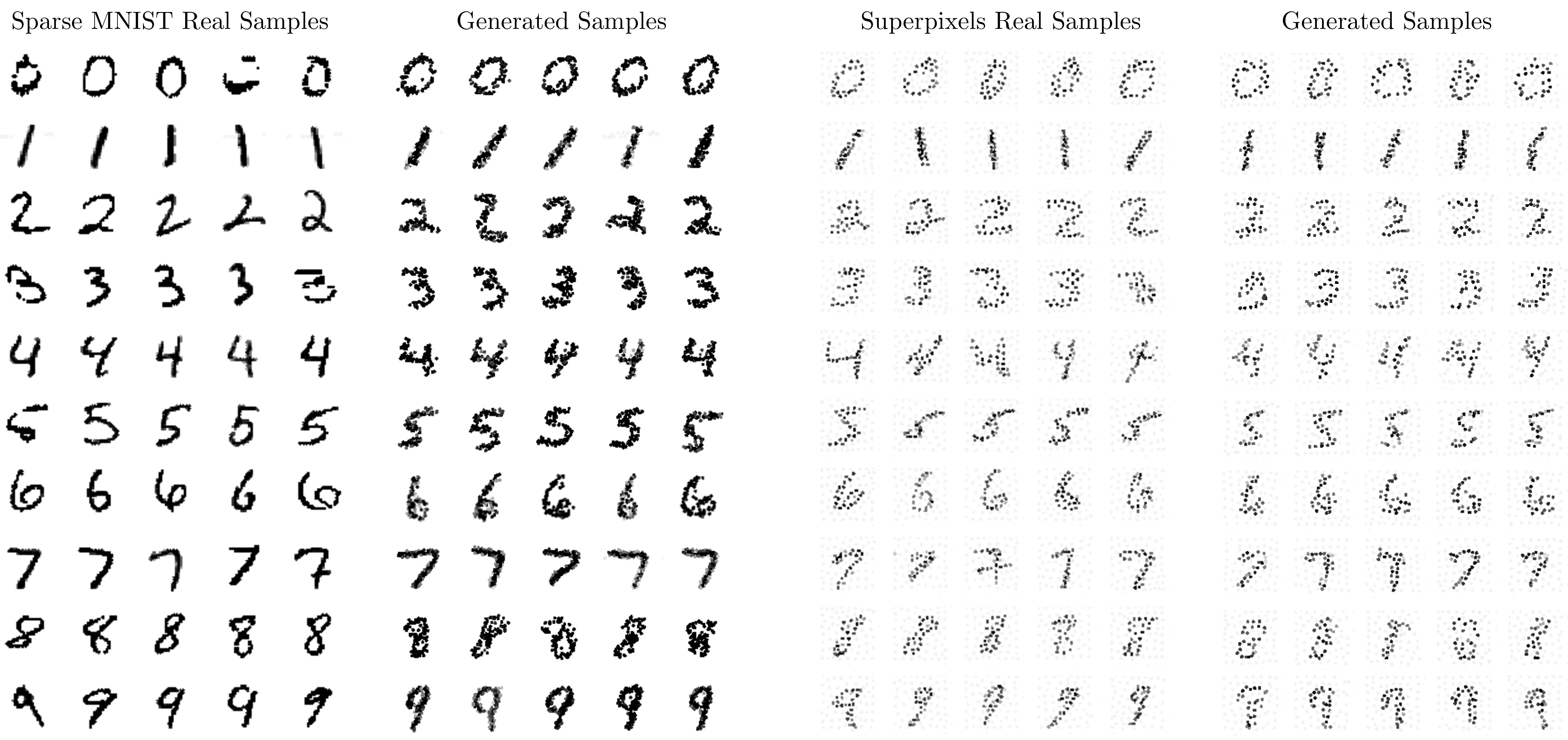
Before applying MPGAN to the JetNet dataset, we test it initially on point-cloud versions of the MNIST handwritten digits dataset [329]. Practically, these were highly useful during the development of the model, while exploring architectures, hyperparameters, and training strategies, as they provided a simpler test-bench as well as an easy way to visually evaluate the model.

We consider two MNIST datasets. First, a sparse graph representation of the MNIST dataset, where from each image we select the 100 highest intensity pixels as the nodes of a fully connected graph, with their feature vectors consisting of the $x$, $y$ coordinates and intensities. This is directly analogous to selecting the coordinates and momenta of the highest momentum particles in a jet or highest energy hits in a detector. The second dataset, known as the MNIST superpixels dataset [328], was created by converting each MNIST image into 75 superpixels, corresponding to the nodes of a graph. The centers and intensities of the superpixels comprise the hidden features of the nodes.

We train MPGAN separately for each digit, analogous to independent trainings for different jet classes. The best parameters per-digit are chosen using a variation of FID adopted for point clouds, using the hidden features of the MoNet classifier [328]. The comparison between the real and MPGAN-generated samples for both datasets can be seen in Figure 10.2. We observe that the model is able to reproduce the real samples with high fidelity and little evidence of mode dropping.

10.1.4 Experiments on jets

We now present results on the JetNet dataset. We first discuss the evaluation metrics, then the results of the MPGAN model compared to several baseline point-cloud generative models, as well as extensive discussion on both the architecture and evaluation metric choices.

Evaluation

We use four techniques discussed in Section 10.1.1 for evaluating and comparing models. Distributions of physical particle and jet features are compared visually and quantitatively using the Wasserstein-1 ($W_1$) distance between them. For ease of evaluation, we report (1) the average scores of the three particle features ($W_1^P$) ${\eta }^{\mathrm{rel}}$, ${\varphi }^{\mathrm{rel}}$, and $p_T^{\mathrm{rel}}$, (2) the jet mass ($W_1^M$), and (3) the average of a subset of the EFPs¹ ($W_1^{\mathrm{EFP}}$), which together provide a holistic picture of the low- and high-level aspects of a jet. The $W_1$ distances are calculated for each feature between random samples of 10,000 real and generated jets, and averaged over 5 batches. Baseline $W_1$ distances are calculated between two sets of randomly sampled real jets with 10,000 samples each, and are listed for each feature in Table 10.1. The real samples are split 70/30 for training/evaluation. We train ParticleNet for classification on our dataset to develop the FPND metric. FPND is calculated between 50,000 random real and generated samples, based on the activations of the first FC layer in our trained model². Coverage and MMD are calculated between 100 real and 100 generated samples, and averaged over 10 such batches. Implementations for all metrics are provided in the JetNet package [330].

Results

On each of JetNet’s three classes, we test r-GAN’s FC, GraphCNN, and TreeGAN generators with rGAN’s FC and the PointNet-Mix discriminators, and compare them to MPGAN’s MP generator and discriminator models, including both MP and MP-LFC generator variations. Training and implementation details for each can be found in Appendix C.1.2, and all code in Ref. [331]. We use a maximum of 30 particles per jet, choosing the 30 highest-$p_T$ particles in jets with more than 30.

We choose model parameters which, during training, yield the lowest $W_1^M$ score. This is because (1) $W_1$ scores between physical features are more relevant for physics applications than the other three metrics, and (2) qualitatively we find it be a better discriminator of model quality than particle features or EFP scores. Table 10.2 lists the scores for each model and class, and Figure 10.3 shows plots of selected feature distributions of real and generated jets, for the best performing FC, GraphCNN, TreeGAN, and MP generators. We also provide discretized images in the angular-coordinates-plane, a.k.a “jet images”, in Figures 10.4—10.6; however, we note that it is in general not easy to visually evaluate the quality of individual particle clouds, hence we focus on metrics and visualizations aggregated over batches of clouds. Overall we find that MPGAN is a significant improvement over the best FC, GraphCNN, and TreeGAN models, particularly for top and light quark jets. This is evident both visually and quantitatively in every metric, especially jet $W_1$s and FPND, with the exception of $W_1^P$ where only the FC generator and PointNet discriminator (FC + PointNet) combination is more performant.

We additionally perform a latency measurement and find, using an NVIDIA A100 GPU, that MPGAN generation requires $35.7\mu$s per jet. In comparison, the traditional generation process for JetNet is measured on an 8-CPU machine as requiring 46ms per jet, meaning MPGAN provides a three-orders-of-magnitude speed-up. Furthermore, as noted in Section 9.2, the generation of JetNet is significantly simpler than full simulation and reconstruction used at the LHC, which has been measured to require 12.3s [311] and 4s [332] respectively per top quark jet. Hence in practical applications we anticipate MPGAN’s improvement to potentially rise to five-orders-of-magnitude.

Real baseline comparison

We find that MPGAN’s jet-level $W_1$ scores all fall within error of the baselines in Table 10.1, while those of alternative generators are several standard deviations away. This is particularly an issue with complex top quark particle clouds, where we can see in Figure 10.3 none of the existing generators are able to learn the bimodal jet feature distributions, and smaller light quark clouds, where we see distortion of jet features due to difficulty reproducing the zero-padded particle features. No model is able to achieve particle-level scores close to the baseline, and only those of the FC + PointNet combination and MPGAN are of the same order of magnitude. We conclude that MPGAN reproduces the physical observable distributions to the highest degree of accuracy, but note, however, that it requires further improvement in particle feature reconstruction before it is ready for practical application in HEP.

Architecture discussion

To disentangle the effectiveness of the MP generator and discriminator, we train each individually with alternative counterparts (Table 10.2). With the same PointNet discriminator, the GraphCNN and TreeGAN generators perform worse than the simple FC generator for every metric on all three datasets. The physics-motivated MP generator on the other hand outperforms all on the gluon and top quark datasets, and significantly so on the jet-level $W_1$ scores and the FPND. We note, however, that the MP generator is not a significant improvement over the other generators with an FC discriminator. Holding the generator fixed, the PointNet discriminator performs significantly better over the FC for all metrics. With the FC, GraphCNN, and TreeGAN generators, PointNet is also an improvement over the MP discriminator. With an MP generator, the MP discrimimator is more performant on jet-level $W_1$ and FPND scores but, on the top quark dataset, degrades $W_1^P$ relative to PointNet.

We learn from these three things: (1) a generator or discriminator architecture is only as effective as its counterpart—even though the MPGAN combination is the best overall, when paired with a network which is not able to learn complex substructure, or which breaks the permutation symmetry, neither the generator or discriminator is performant, (2) for high-fidelity jet feature reconstruction, both networks must be able to learn complex multi-particle correlations—however, this can come at the cost of low-level feature accuracy, and (3) MPGAN’s masking strategy is highly effective as both MP networks are improvements all around on light quark jets.

Particle cloud evaluation metrics

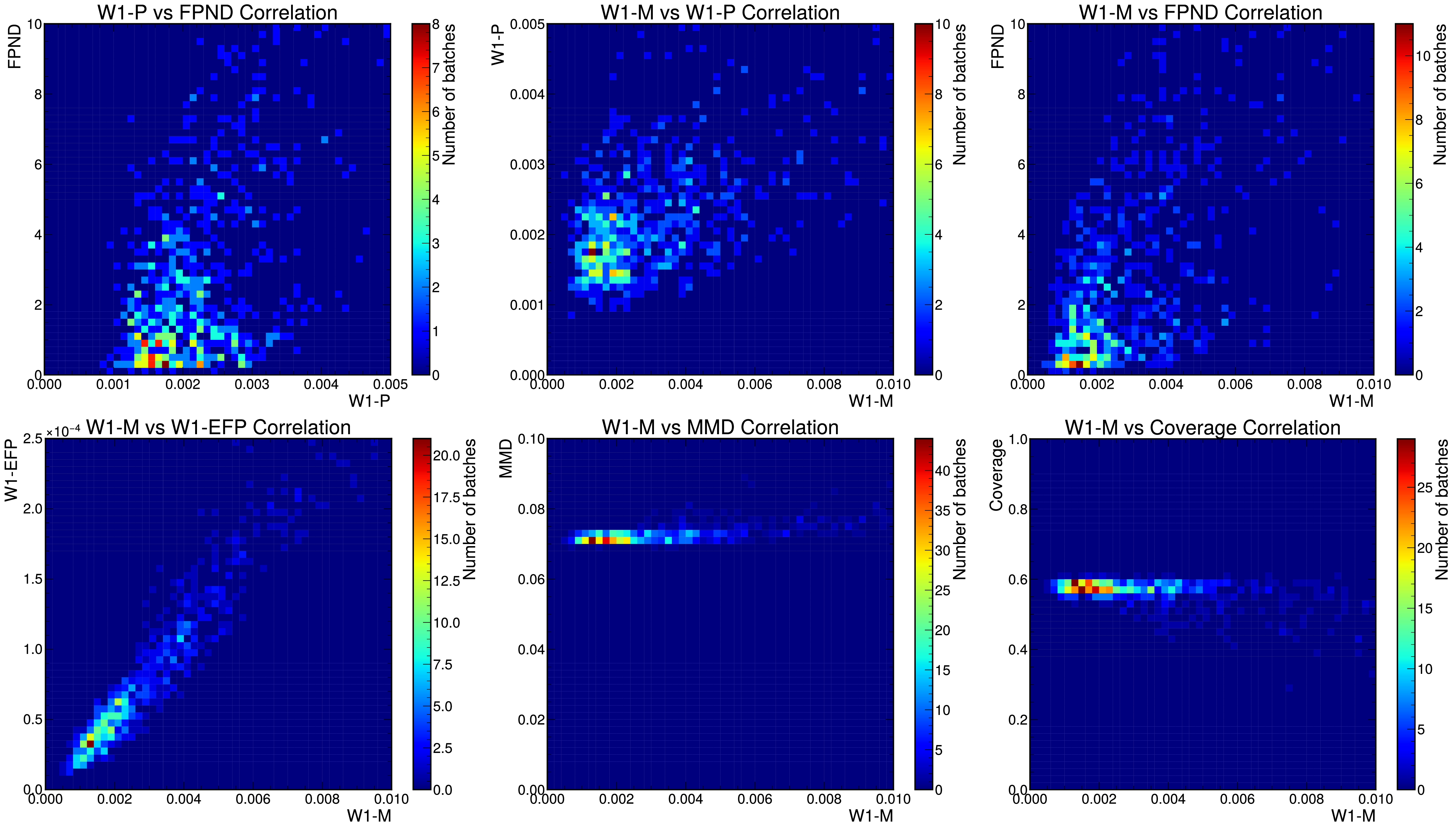
We now discuss the merits of each evaluation metrics and provide suggestions for their use in future work. Figure 10.7 shows correlation plots between chosen pairs of our evaluation metrics. As expected, we find W1-M and W1-EFP to be highly correlated, as they both measure learning of global jet features. For rigorous validation we suggest measuring both but for time-sensitive use-cases, such as quick evaluations during model training, W1-M should be sufficient. W1-M, FPND, and W1-P are all measuring different aspects of the generation and are relatively uncorrelated. We expect FPND overall to be the best and most discriminatory metric for evaluation, as it compares features found by a SOTA classifier to be statistically optimum for characterizing jets, while the W1 scores are valuable for their interpretability. Out of these, W1-M/W1-EFP are the most important from a physics-standpoint, as we generally characterize collisions by the high-level features of the output jets, rather than the individual particle features.

MMD and coverage are both valuable for specifically evaluating the quality and diversity of samples respectively, however we see from Figure 10.7 that they saturate after a certain point, after which FPND and $W_1$ scores are necessary for stronger discrimination. We also note that in Table 10.2, models with low $W_1$ scores relative to the baseline have the best coverage and MMD scores as well. This indicates that the $W_1$ metrics are sensitive to both mode collapse (measured by coverage), which is expected as in terms of feature distributions mode collapse manifests as differing supports, to which the $W_1$ distance is sensitive, as well as to individual sample quality (measured by MMD), which supports our claim that recovering jet feature distributions implies accurate learning of individual cloud structure. Together this suggests that low $W_1$ scores are able to validate sample quality and against mode collapse, and justifies our criteria that a practical ML simulation alternative have $W_1$ scores close to the baselines in Table 10.2. In conclusion, for thorough validation of generated particle clouds, we recommend considering all three W-1 scores in conjunction with FPND, while MMD and coverage, being focused tests of these aspects of generation, may be useful for understanding failure modes during model development.

10.1.5 Summary

In this section, we applied existing state-of-the-art point cloud generative models to JetNet, and proposed several physics- and computer-vision-inspired metrics to rigorously evaluate generated clouds. We found that existing models are not performant on a number of metrics, and failed to reproduce high-level jet features—arguably the most significant aspect for HEP. We then introduced the novel message-passing generative adversarial network (MPGAN) model, designed to capture complex global structure and handle variable-sized clouds, which significantly improved performance in this area, as well as other metrics.

Despite the high performance, the major limitation of MPGAN is the quadratic scaling of the message passing operation, which makes it difficult to scale to larger clouds than 30-particle ones used in Section 10.1.4. In the next section, we discuss the iGAPT model to overcome this limitation.